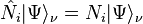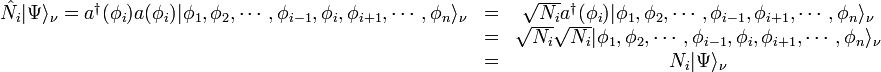Particle number operator

In quantum mechanics, for systems where the total number of particles may not be preserved, the number operator is the observable that counts the number of particles.

The number operator acts on Fock space. Let

|\Psi\rangle_\nu=|\phi_1,\phi_2,\cdots,\phi_n\rangle_\nu

be a Fock state, composed of single-particle states 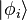|\phi_i\rangle drawn from a basis of the underlying Hilbert space of the Fock space. Given the corresponding creation and annihilation operators a^{\dagger}(\phi_i) and a(\phi_i)\, we define the number operator by

\hat{N_i} \ \stackrel{\mathrm{def}}{=}\ a^{\dagger}(\phi_i)a(\phi_i)

and we have

\hat{N_i}|\Psi\rangle_\nu=N_i|\Psi\rangle_\nu

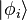where N_i is the number of particles in state |\phi_i\rangle. The above equality can be proven by noting that

\begin{matrix} a(\phi_i) |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_i,\phi_{i+1},\cdots,\phi_n\rangle_\nu &=& \sqrt{N_i} |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_{i+1},\cdots,\phi_n\rangle_\nu \\ a^{\dagger}(\phi_i) |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_{i+1},\cdots,\phi_n\rangle_\nu &=& \sqrt{N_i} |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_{i},\phi_{i+1},\cdots,\phi_n\rangle_\nu \end{matrix}

then

\begin{matrix} \hat{N_i}|\Psi\rangle_\nu = a^{\dagger}(\phi_i)a(\phi_i) |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_i,\phi_{i+1},\cdots,\phi_n\rangle_\nu &=& \sqrt{N_i} a^{\dagger}(\phi_i) |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_{i+1},\cdots,\phi_n\rangle_\nu \\ &=& \sqrt{N_i} \sqrt{N_i} |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_{i},\phi_{i+1},\cdots,\phi_n\rangle_\nu \\&=& N_i|\Psi\rangle_\nu\\ \end{matrix}

See also

References


This article is issued from Wikipedia - version of the Saturday, April 25, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.