Symmetric inverse semigroup

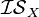In abstract algebra, the set of all partial bijections on a set X (aka one-to-one partial transformations) forms an inverse semigroup, called the symmetric inverse semigroup[1] (actually a monoid) on X. The conventional notation for the symmetric inverse semigroup on a set X is \mathcal{I}_X[2] or \mathcal{IS}_X[3] In general \mathcal{I}_X is not commutative.

Details about the origin of the symmetric inverse semigroup are available in the discussion on the origins of the inverse semigroup.

Finite symmetric inverse semigroups

When X is a finite set {1, ..., n}, the inverse semigroup of one-one partial transformations is denoted by Cn and its elements are called charts or partial symmetries.[4] The notion of chart generalizes the notion of permutation. A (famous) example of (sets of) charts are the hypomorphic mapping sets from the reconstruction conjecture in graph theory.[5]

The cycle notation of classical, group-based permutations generalizes to symmetric inverse semigroups by the addition of a notion called a path, which (unlike a cycle) ends when it reaches the "undefined" element; the notation thus extended is called path notation.[6]

See also

Notes

  1. ↑ Pierre A. Grillet (1995). Semigroups: An Introduction to the Structure Theory. CRC Press. p. 228. ISBN 978-0-8247-9662-4.
  2. ↑ Hollings 2014, p. 252
  3. ↑ Ganyushkin and Mazorchuk 2008, p. v
  4. ↑ Lipscomb 1997, p. 1
  5. ↑ Lipscomb 1997, p. xiii
  6. ↑ Lipscomb 1997, p. xiii

References

This article is issued from Wikipedia - version of the Thursday, August 28, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.