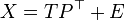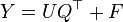Partial least squares regression
| Part of a series on Statistics |
| Regression analysis |
|---|
 |
| Models |
| Estimation |
| Background |
|
Partial least squares regression (PLS regression) is a statistical method that bears some relation to principal components regression; instead of finding hyperplanes of minimum variance between the response and independent variables, it finds a linear regression model by projecting the predicted variables and the observable variables to a new space. Because both the X and Y data are projected to new spaces, the PLS family of methods are known as bilinear factor models. Partial least squares Discriminant Analysis (PLS-DA) is a variant used when the Y is categorical.
PLS is used to find the fundamental relations between two matrices (X and Y), i.e. a latent variable approach to modeling the covariance structures in these two spaces. A PLS model will try to find the multidimensional direction in the X space that explains the maximum multidimensional variance direction in the Y space. PLS regression is particularly suited when the matrix of predictors has more variables than observations, and when there is multicollinearity among X values. By contrast, standard regression will fail in these cases (unless it is regularized).
The PLS algorithm is employed in partial least squares path modeling,[1][2] a method of modeling a "causal" network of latent variables (causes cannot be determined without experimental or quasi-experimental methods, but one typically bases a latent variable model on the prior theoretical assumption that latent variables cause manifestations in their measured indicators). This technique is argued to be a form of structural equation modeling, distinguished from the classical method by being component-based rather than covariance-based.[3] Yet, others dispute that this is the case.[4]
Partial least squares was introduced by the Swedish statistician Herman Wold, who then developed it with his son, Svante Wold. An alternative term for PLS (and more correct according to Svante Wold[5]) is projection to latent structures, but the term partial least squares is still dominant in many areas. Although the original applications were in the social sciences, PLS regression is today most widely used in chemometrics and related areas. It is also used in bioinformatics, sensometrics, neuroscience and anthropology. In contrast, PLS path modeling is most often used in social sciences, econometrics, marketing and strategic management. However, within the realm of psychology, it has received criticism for being an unreliable estimation and testing tool.[4]
Underlying model
The general underlying model of multivariate PLS is
where  is an
is an  matrix of predictors,
matrix of predictors, 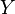 is an
is an 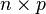 matrix of responses;
matrix of responses;  and
and 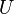 are
are  matrices that are, respectively, projections of
matrices that are, respectively, projections of  (the X score, component or factor matrix) and projections of
(the X score, component or factor matrix) and projections of 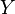 (the Y scores);
(the Y scores);  and
and 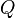 are, respectively,
are, respectively,  and
and 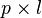 orthogonal loading matrices; and matrices
orthogonal loading matrices; and matrices 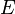 and
and  are the error terms, assumed to be independent and identically distributed random normal variables. The decompositions of
are the error terms, assumed to be independent and identically distributed random normal variables. The decompositions of  and
and 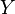 are made so as to maximise the covariance between
are made so as to maximise the covariance between  and
and 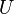 .
.
Algorithms
A number of variants of PLS exist for estimating the factor and loading matrices  and
and 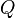 . Most of them construct estimates of the linear regression between
. Most of them construct estimates of the linear regression between  and
and 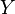 as
as  . Some PLS algorithms are only appropriate for the case where
. Some PLS algorithms are only appropriate for the case where 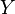 is a column vector, while others deal with the general case of a matrix
is a column vector, while others deal with the general case of a matrix 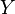 . Algorithms also differ on whether they estimate the factor matrix
. Algorithms also differ on whether they estimate the factor matrix  as an orthogonal, an orthonormal matrix or not.[6][7][8][9][10][11]
The final prediction will be the same for all these varieties of PLS, but the components will differ.
as an orthogonal, an orthonormal matrix or not.[6][7][8][9][10][11]
The final prediction will be the same for all these varieties of PLS, but the components will differ.
PLS1
PLS1 is a widely used algorithm appropriate for the vector Y case. It estimates T as an orthonormal matrix. In pseudocode it is expressed below (capital letters are matrices, lower case letters are vectors if they are superscripted and scalars if they are subscripted):
1 function PLS1() 2
3
, an initial estimate of w. 4
5 for
to l 6
(note this is a scalar) 7
8
9
(note this is a scalar) 10 if
11
, break the for loop 12 if
13
14
15
16 end for 17 define W to be the matrix with columns
. Do the same to form the P matrix and q vector. 18
19
20 return
This form of the algorithm does not require centering of the input X and Y, as this is performed implicitly by the algorithm.
This algorithm features 'deflation' of the matrix X (subtraction of 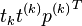 ), but deflation of the vector y is not performed, as it is not necessary (it can be proved that deflating y yields the same results as not deflating.). The user-supplied variable l is the limit on the number of latent factors in the regression; if it equals the rank of the matrix X, the algorithm will yield the least squares regression estimates for B and
), but deflation of the vector y is not performed, as it is not necessary (it can be proved that deflating y yields the same results as not deflating.). The user-supplied variable l is the limit on the number of latent factors in the regression; if it equals the rank of the matrix X, the algorithm will yield the least squares regression estimates for B and 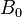
Extensions
In 2002 a new method was published called orthogonal projections to latent structures (OPLS). In OPLS, continuous variable data is separated into predictive and uncorrelated information. This leads to improved diagnostics, as well as more easily interpreted visualization. However, these changes only improve the interpretability, not the predictivity, of the PLS models.[12] L-PLS extends PLS regression to 3 connected data blocks.[13] Similarly, OPLS-DA (Discriminant Analysis) may be applied when working with discrete variables, as in classification and biomarker studies.
Software implementation
Most major statistical software packages offer PLS regression. The 'pls' package in R provides a range of algorithms.[14]
See also
- Feature extraction
- Data mining
- Machine learning
- Regression analysis
- Canonical correlation
- Deming regression
- Multilinear subspace learning
- Principal component analysis
- Total sum of squares
Further reading
- Kramer, R. (1998). Chemometric Techniques for Quantitative Analysis. Marcel-Dekker. ISBN 0-8247-0198-4.
- Frank, Ildiko E.; Friedman, Jerome H. (1993). "A Statistical View of Some Chemometrics Regression Tools". Technometrics 35 (2): 109–148. doi:10.1080/00401706.1993.10485033.
- Haenlein, Michael; Kaplan, Andreas M. (2004). "A Beginner's Guide to Partial Least Squares Analysis". Understanding Statistics 3 (4): 283–297. doi:10.1207/s15328031us0304_4.
- Henseler, Joerg; Fassott, Georg (2005). "Testing Moderating Effects in PLS Path Models. An Illustration of Available Procedures".
- Lingjærde, Ole-Christian; Christophersen, Nils (2000). "Shrinkage Structure of Partial Least Squares". Scandinavian Journal of Statistics 27 (3): 459–473. doi:10.1111/1467-9469.00201.
- Tenenhaus, Michel (1998). La Régression PLS: Théorie et Pratique. Paris: Technip.
- Rosipal, Roman; Kramer, Nicole (2006). "Overview and Recent Advances in Partial Least Squares, in Subspace, Latent Structure and Feature Selection Techniques": 34–51.
- Helland, Inge S. (1990). "PLS regression and statistical models". Scandinavian Journal of Statistics 17 (2): 97–114. JSTOR 4616159.
- Wold, Herman (1966). "Estimation of principal components and related models by iterative least squares". In Krishnaiaah, P.R. Multivariate Analysis. New York: Academic Press. pp. 391–420.
- Wold, Herman (1981). The fix-point approach to interdependent systems. Amsterdam: North Holland.
- Wold, Herman (1985). "Partial least squares". In Kotz, Samuel; Johnson, Norman L. Encyclopedia of statistical sciences 6. New York: Wiley. pp. 581–591.
- Wold, Svante; Ruhe, Axel; Wold, Herman; Dunn, W.J. (1984). "The collinearity problem in linear regression. the partial least squares (PLS) approach to generalized inverses". SIAM Journal on Scientific and Statistical Computing 5 (3): 735–743. doi:10.1137/0905052.
- Garthwaite, Paul H. (1994). "An Interpretation of Partial Least Squares". Journal of the American Statistical Association 89 (425): 122–7. doi:10.1080/01621459.1994.10476452. JSTOR 2291207.
- Wang, H., ed. (2010). Handbook of Partial Least Squares. ISBN 978-3-540-32825-4.
- Stone, M.; Brooks, R.J. (1990). "Continuum Regression: Cross-Validated Sequentially Constructed Prediction embracing Ordinary Least Squares, Partial Least Squares and Principal Components Regression". Journal of the Royal Statistical Society, Series B 52 (2): 237–269. JSTOR 2345437.
- Wan Mohamad Asyraf Bin Wan Afthanorhan. (2013). A Comparison Of Partial Least Square Structural Equation Modeling (PLS-SEM) and Covariance Based Structural EquationModeling (CB-SEM) for Confirmatory Factor Analysis International Journal of Engineering Science and Innovative Technology (IJESIT), 2(5), 9.
References
- ↑ Tenenhaus, M.; Esposito Vinzi, V.; Chatelinc, Y-M.; Lauro, C. (January 2005). "PLS path modeling" (PDF). Computational Statistics & Data Analysis 48 (1): 159–205. doi:10.1016/j.csda.2004.03.005.
- ↑ Vinzi, V.; Chin, W.W.; Henseler, J.; et al., eds. (2010). Handbook of Partial Least Squares. ISBN 978-3-540-32825-4.
- ↑ Tenenhaus, M. (2008). "Component-based structural equation modelling" (PDF).
- 1 2 Rönkkö, M.; McIntosh, C.; Antonakis, J. (2015). "On the adoption of partial least squares in psychological research: Caveat emptor". Personality and Individual Differences. pp. 76–84. doi:10.1016/j.paid.2015.07.019.
- ↑ Wold, S; Sjöström, M.; Eriksson, L. (2001). "PLS-regression: a basic tool of chemometrics". Chemometrics and Intelligent Laboratory Systems 58 (2): 109–130. doi:10.1016/S0169-7439(01)00155-1.
- ↑ Lindgren, F; Geladi, P; Wold, S (1993). "The kernel algorithm for PLS". J. Chemometrics 7: 45–59. doi:10.1002/cem.1180070104.
- ↑ de Jong, S.; ter Braak, C.J.F. (1994). "Comments on the PLS kernel algorithm". J. Chemometrics 8 (2): 169–174. doi:10.1002/cem.1180080208.
- ↑ Dayal, B.S.; MacGregor, J.F. (1997). "Improved PLS algorithms". J. Chemometrics 11 (1): 73–85. doi:10.1002/(SICI)1099-128X(199701)11:1<73::AID-CEM435>3.0.CO;2-#.
- ↑ de Jong, S. (1993). "SIMPLS: an alternative approach to partial least squares regression". Chemometrics and Intelligent Laboratory Systems 18 (3): 251–263. doi:10.1016/0169-7439(93)85002-X.
- ↑ Rannar, S.; Lindgren, F.; Geladi, P.; Wold, S. (1994). "A PLS Kernel Algorithm for Data Sets with Many Variables and Fewer Objects. Part 1: Theory and Algorithm". J. Chemometrics 8 (2): 111–125. doi:10.1002/cem.1180080204.
- ↑ Abdi, H. (2010). "Partial least squares regression and projection on latent structure regression (PLS-Regression)". Wiley Interdisciplinary Reviews: Computational Statistics 2: 97–106. doi:10.1002/wics.51.
- ↑ Trygg, J; Wold, S (2002). "Orthogonal Projections to Latent Structures". Journal of Chemometrics 16 (3): 119–128. doi:10.1002/cem.695.
- ↑ Sæbøa, S.; Almøya, T.; Flatbergb, A.; Aastveita, A.H.; Martens, H. (2008). "LPLS-regression: a method for prediction and classification under the influence of background information on predictor variables". Chemometrics and Intelligent Laboratory Systems 91 (2): 121–132. doi:10.1016/j.chemolab.2007.10.006.
- ↑ "Package ‘pls’" (PDF).
External links
- imDEV free Excel add-in for PLS and PLS-DA
- PLS in Brain Imaging
- on-line PLS regression (PLSR) at Virtual Computational Chemistry Laboratory
- Uncertainty estimation for PLS
- A short introduction to PLS regression and its history
|