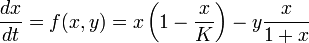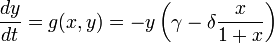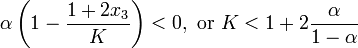Paradox of enrichment
The paradox of enrichment is a term from population ecology coined by Michael Rosenzweig in 1971. He described an effect in six predator-prey models wherein increasing the food available to the prey caused the predator's population to destabilize. A common example is that if the food supply of a prey such as a rabbit is overabundant, its population will grow unbounded and cause the predator population (such as a lynx) to grow unsustainably large. This may result in a crash in the population of the predators and possibly lead to local eradication or even species extinction.
The term 'paradox' has been used since then to describe this effect in slightly conflicting ways. The original sense was one of irony; that by attempting to increase carrying capacity in an ecosystem, one could fatally imbalance it. Since then, some authors have used the word to describe the difference between modelled and real predator-prey interactions.
Rosenzweig's result (Rosenzweig 1971)
Rosenzweig used ordinary differential equation models to simulate the prey population. Models only represented prey populations. Enrichment was taken to be increasing the prey carrying capacity and showing that the prey population destabilized, usually into a limit cycle.
The cycling behavior after destabilization was more thoroughly explored in a subsequent paper (May 1972) and discussion (Gilpin and Rozenzweig 1972).
Model and Exception
Many studies have been done on the paradox of enrichment since Rosenzweig, and some have shown that the model initially proposed does not hold in all circumstances, as summarised by Roy and Chattopadhyay in 2007. Cases where the paradox of enrichment may not apply include the following:
- inedible prey: if there are multiple prey species, and not all are edible, then some may absorb nutrients and stabilise cyclicity.
- invulnerable prey: even with a single prey species, if there is a degree of temporal or spatial refuge (i.e. the prey can hide from the predator), then destabilisation may not happen
- unpalatable prey: if prey do not fulfil the nutritional preferences of the predator to as great an extent at higher densities, as with some algae and grazers, then there may be a stabilising effect
- heterogeneous environment: the model for enrichment follows an assumption of environmental homogeneity. If a spatiotemporally chaotic, heterogeneous environment is introduced, then cyclic patterns may not arise
- induced defense: if there is a predation-dependent response from prey species, then it may act to decelerate the downward swing of population caused by the boom in predator population. An example is of Daphnia and fish predators.
- autotoxins and other predator density-dependent effects: If predator density cannot increase in proportion to that of prey, then destabilising periodicities may not develop.
- prey toxicity: if there is a significant cost to the predator of consuming the (now highly-dense) prey species, then predator numbers may not increase sufficiently to give periodicity
Link with the Hopf bifurcation
The paradox of enrichment can be accounted for by the bifurcation theory. As the carrying capacity increases, the equilibrium of the dynamical system becomes unstable.
The bifurcation can be obtained by modifying the Lotka-Volterra equation. First, one assumes that the growth of the prey population is determined by the logistic equation. Second, one assumes that predators have a non-linear functional response, typically of type II. The saturation in consumption may be caused by the time to handle the prey or satiety effects.
Thus, one can write the following (normalized) equations:
- x is the prey density;
- y is the predator density;
- K is the prey population's carrying capacity;
- γ and δ are predator population's parameters (rate of decay and benefits of consumption, respectively).
The term 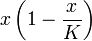 represents the prey's logistic growth, and
represents the prey's logistic growth, and 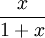 the predator's functional response.
the predator's functional response.
The prey isoclines (points at which the prey population does not change, i.e. dx/dt = 0) are easily obtained as 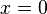 and
and  . Likewise, the predator isoclines are obtained as
. Likewise, the predator isoclines are obtained as 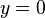 and
and 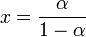 , where
, where 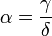 . The intersections of the isoclines yields three equilibrium states:
. The intersections of the isoclines yields three equilibrium states:
The first equilibrium corresponds to the extinction of both predator and prey, the second one to the extinction of the predator, and the third to co-existence.
The standard method to determine the stability of the steady states is to approximate the non-linear system by a linear system which can be solved in closed form. After differentiating  and
and  with respect to
with respect to  and
and 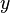 in a neighborhood of
in a neighborhood of 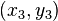 , we get:
, we get:
It is possible to find the exact solution of this linear system, but here, we are only interested in the qualitative behavior. It is a classical result of linear systems that if both eigenvalues of the matrix are real and negative, the system converges to a limit point. Since the determinant is equal to the product of the eigenvalues and is positive, both eigenvalues have the same sign. Since the trace is equal to the sum of the eigenvalues, the system is stable if:
At this critical value of the parameter K, the system undergoes a Hopf bifurcation. This comes as counter-intuitive (hence the term 'paradox') because increasing the carrying capacity of the ecological system beyond a certain value leads to dynamic instability, and extinction of the predator species.
Arguments against the paradox
A credible, simple alternative to the Lotka-Volterra predator-prey model and its common prey dependent generalizations is the ratio dependent or Arditi-Ginzburg model.[1] The two are the extremes of the spectrum of predator interference models. According to the authors of the alternative view, the data show that true interactions in nature are so far from the Lotka-Volterra extreme on the interference spectrum that the model can simply be discounted as wrong. They are much closer to the ratio dependent extreme, so if a simple model is needed one can use the Arditi-Ginzburg model as the first approximation.[2]
The presence of the paradox is strongly dependent on the assumption of the prey dependence of the functional response; because of this the ratio dependent Arditi-Ginzburg model, does not have the paradoxical behavior. These authors argued that the absence of the paradox in nature (simple laboratory systems may be the exception) is in fact a strong argument for their alternative view of the basic equations.[3]
See also
- Braess' paradox: Adding extra capacity to a network may reduce overall performance.
- Paradox of the pesticides: Applying pesticide may increase the pest population.
References
- ↑ Arditi, R. and Ginzburg, L.R. (1989) "Coupling in predator-prey dynamics: ratio dependence" Journal of Theoretical Biology, 139: 311–326.
- ↑ Arditi, R. and Ginzburg, L.R. (2012) How Species Interact: Altering the Standard View on Trophic Ecology Oxford University Press. ISBN 9780199913831.
- ↑ Jensen, C. XJ., and Ginzburg, L.R. (2005) "Paradoxes or theoretical failures? The jury is still out." Ecological Modeling, 118:3–14.
Other reading
- Gilpin, Michael and Michael Rosenzweig. 1972. "Enriched Predator-Prey Systems: Theoretical Stability" Science Vol. 177, pp. 902–904.
- May, Robert. 1972. "Limit Cycles in Predator-Prey Communities" Science Vol. 177, pp. 900–902.
- Rosenzweig, Michael. 1971. "The Paradox of Enrichment" Science Vol. 171: pp. 385–387
- Kot, Mark. 2001. "Elements of Mathematical Ecology" Cambridge University Press
- Roy, Shovonlal; J Chattopadhyay (2007). "The stability of ecosystems: A brief overview of the paradox of enrichment". Journal of Biosciences 32 (2): 421–428. doi:10.1007/s12038-007-0040-1. ISSN 0250-5991. Retrieved 2010-12-08.