Papkovich–Neuber solution

The Papkovich–Neuber solution is a technique for generating analytic solutions to the Newtonian incompressible Stokes equations, though it was originally developed to solve the equations of linear elasticity.

It can be shown that any Stokes flow with body force 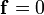$\mathbf{f}=0$ can be written in the form:

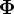\mathbf{u} = {1\over{2 \mu}} \left[ \nabla ( \mathbf{x} \cdot \mathbf{\Phi} + \chi) - 2 \mathbf{\Phi} \right]

p = \nabla \cdot \mathbf{\Phi}

where $\mathbf{\Phi}$ is a harmonic vector potential and $\chi$ is a harmonic scalar potential. The properties and ease of construction of harmonic functions makes the Papkovich–Neuber solution a powerful technique for solving the Stokes Equations in a variety of domains.

References

Neuber, H. (1934), "Ein neuer Ansatz zur Lösung räumlicher Probleme der Elastizitätstheorie", Journal of Applied Mathematics and Mechanics 14, pp. 203–212, doi:10.1002/zamm.19340140404 .
Papkovish, P. F. (1932), "Solution Générale des équations differentielles fondamentales d'élasticité exprimée par trois fonctions harmoniques", Compt. Rend. Acad. Sci. Paris 195, pp. 513–515 .

This article is issued from Wikipedia - version of the Saturday, April 20, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.