Paley–Zygmund inequality

In mathematics, the Paley–Zygmund inequality bounds the probability that a positive random variable is small, in terms of its mean and variance (i.e., its first two moments). The inequality was proved by Raymond Paley and Antoni Zygmund.

Theorem: If Z ≥ 0 is a random variable with finite variance, and if 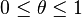$0 \le \theta \le 1$ , then

\operatorname{P}( Z > \theta\operatorname{E}[Z] ) \ge (1-\theta)^2 \frac{\operatorname{E}[Z]^2}{\operatorname{E}[Z^2]}.

Proof: First,

\operatorname{E}[Z] = \operatorname{E}[ Z \, \mathbf{1}_{\{ Z \le \theta \operatorname{E}[Z] \}}] + \operatorname{E}[ Z \, \mathbf{1}_{\{ Z > \theta \operatorname{E}[Z] \}} ].

The first addend is at most $\theta \operatorname{E}[Z]$ , while the second is at most $\operatorname{E}[Z^2]^{1/2} \operatorname{P}( Z > \theta\operatorname{E}[Z])^{1/2}$ by the Cauchy–Schwarz inequality. The desired inequality then follows. ∎

Related inequalities

The Paley–Zygmund inequality can be written as

\operatorname{P}( Z > \theta \operatorname{E}[Z] ) \ge \frac{(1-\theta)^2 \, \operatorname{E}[Z]^2}{\operatorname{Var} Z + \operatorname{E}[Z]^2}.

This can be improved. By the Cauchy–Schwarz inequality,

\operatorname{E}[Z - \theta \operatorname{E}[Z]] \le \operatorname{E}[ (Z - \theta \operatorname{E}[Z]) \mathbf{1}_{\{ Z > \theta \operatorname{E}[Z] \}} ] \le \operatorname{E}[ (Z - \theta \operatorname{E}[Z])^2 ]^{1/2} \operatorname{P}( Z > \theta \operatorname{E}[Z] )^{1/2}

which, after rearranging, implies that

\operatorname{P}(Z > \theta \operatorname{E}[Z]) \ge \frac{(1-\theta)^2 \operatorname{E}[Z]^2}{\operatorname{E}[( Z - \theta \operatorname{E}[Z] )^2]} = \frac{(1-\theta)^2 \operatorname{E}[Z]^2}{\operatorname{Var} Z + (1-\theta)^2 \operatorname{E}[Z]^2}.

This inequality is sharp; equality is achieved if Z almost surely equals a positive constant, for example.

References

R. E. A. C. Paley and A. Zygmund, "On some series of functions, (3)," Proc. Camb. Phil. Soc. 28 (1932), 190-205, (cf. Lemma 19 page 192).

R. E. A. C. Paley and A. Zygmund, A note on analytic functions in the unit circle, Proc. Camb. Phil. Soc. 28 (1932), 266–272

This article is issued from Wikipedia - version of the Monday, August 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.