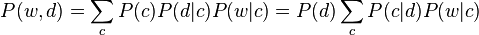Probabilistic latent semantic analysis
Probabilistic latent semantic analysis (PLSA), also known as probabilistic latent semantic indexing (PLSI, especially in information retrieval circles) is a statistical technique for the analysis of two-mode and co-occurrence data. In effect, one can derive a low-dimensional representation of the observed variables in terms of their affinity to certain hidden variables, just as in latent semantic analysis, from which PLSA evolved.
Compared to standard latent semantic analysis which stems from linear algebra and downsizes the occurrence tables (usually via a singular value decomposition), probabilistic latent semantic analysis is based on a mixture decomposition derived from a latent class model.
Model
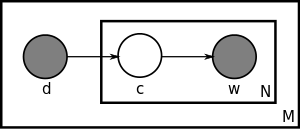
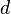 is the document index variable,
is the document index variable,  is a word's topic drawn from the document's topic distribution,
is a word's topic drawn from the document's topic distribution, 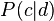 , and
, and  is a word drawn from the word distribution of this word's topic,
is a word drawn from the word distribution of this word's topic, 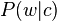 . The
. The 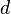 and
and  are observable variables, the topic
are observable variables, the topic  is a latent variable.
is a latent variable.Considering observations in the form of co-occurrences 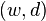 of words and documents, PLSA models the probability of each co-occurrence as a mixture of conditionally independent multinomial distributions:
of words and documents, PLSA models the probability of each co-occurrence as a mixture of conditionally independent multinomial distributions:
being c the words' topic. The first formulation is the symmetric formulation, where  and
and 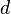 are both generated from the latent class
are both generated from the latent class  in similar ways (using the conditional probabilities
in similar ways (using the conditional probabilities 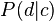 and
and 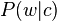 ), whereas the second formulation is the asymmetric formulation, where, for each document
), whereas the second formulation is the asymmetric formulation, where, for each document 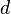 , a latent class is chosen conditionally to the document according to
, a latent class is chosen conditionally to the document according to 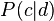 , and a word is then generated from that class according to
, and a word is then generated from that class according to 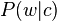 . Although we have used words and documents in this example, the co-occurrence of any couple of discrete variables may be modelled in exactly the same way.
. Although we have used words and documents in this example, the co-occurrence of any couple of discrete variables may be modelled in exactly the same way.
So, the number of parameters is equal to 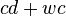 . The number of parameters grows linearly with the number of documents. In addition, although PLSA is a generative model of the documents in the collection it is estimated on, it is not a generative model of new documents.
. The number of parameters grows linearly with the number of documents. In addition, although PLSA is a generative model of the documents in the collection it is estimated on, it is not a generative model of new documents.
Their parameters are learned using the EM algorithm.
Application
PLSA may be used in a discriminative setting, via Fisher kernels.[1]
PLSA has applications in information retrieval and filtering, natural language processing, machine learning from text, and related areas.
It is reported that the aspect model used in the probabilistic latent semantic analysis has severe overfitting problems.[2]
In 2012, pLSA has also been used in the bioinformatics context, for prediction of Gene Ontology biomolecular annotations.[3]
Extensions
- Hierarchical extensions:
- Generative models: The following models have been developed to address an often-criticized shortcoming of PLSA, namely that it is not a proper generative model for new documents.
- Latent Dirichlet allocation - adds a Dirichlet prior on the per-document topic distribution
- Higher-order data: Although this is rarely discussed in the scientific literature, PLSA extends naturally to higher order data (three modes and higher), i.e. it can model co-occurrences over three or more variables. In the symmetric formulation above, this is done simply by adding conditional probability distributions for these additional variables. This is the probabilistic analogue to non-negative tensor factorisation.
History
This is an example of a latent class model (see references therein), and it is related [6] to non-negative matrix factorization. The present terminology was coined in 1999 by Thomas Hofmann.[7]
References and notes
- ↑ Thomas Hofmann, Learning the Similarity of Documents : an information-geometric approach to document retrieval and categorization, Advances in Neural Information Processing Systems 12, pp-914-920, MIT Press, 2000
- ↑ Blei, David M.; Andrew Y. Ng; Michael I. Jordan (2003). "Latent Dirichlet Allocation" (PDF). Journal of Machine Learning Research 3: 993–1022. doi:10.1162/jmlr.2003.3.4-5.993.
- ↑ "Probabilistic Latent Semantic Analysis for prediction of Gene Ontology annotations", Marco Masseroli, Davide Chicco, Pietro Pinoli. IEEE WCCI 2012 - the 2012 IEEE World Congress on Computational Intelligence proceedings. Brisbane, Australia, June 2012. (.pdf)
- ↑ Alexei Vinokourov and Mark Girolami, A Probabilistic Framework for the Hierarchic Organisation and Classification of Document Collections, in Information Processing and Management, 2002
- ↑ Eric Gaussier, Cyril Goutte, Kris Popat and Francine Chen, A Hierarchical Model for Clustering and Categorising Documents, in "Advances in Information Retrieval -- Proceedings of the 24th BCS-IRSG European Colloquium on IR Research (ECIR-02)", 2002
- ↑ Chris Ding, Tao Li, Wei Peng (2006). "Nonnegative Matrix Factorization and Probabilistic Latent Semantic Indexing: Equivalence Chi-Square Statistic, and a Hybrid Method. AAAI 2006
- ↑ Thomas Hofmann, Probabilistic Latent Semantic Indexing, Proceedings of the Twenty-Second Annual International SIGIR Conference on Research and Development in Information Retrieval (SIGIR-99), 1999
See also
- Compound term processing
- Latent Dirichlet allocation
- Latent semantic analysis
- Pachinko allocation
- Vector space model