PKCS 1

The correct title of this article is PKCS #1. The substitution or omission of the # is because of technical restrictions.

In cryptography, PKCS #1 is the first of a family of standards called Public-Key Cryptography Standards (PKCS), published by RSA Laboratories. It provides the basic definitions of and recommendations for implementing the RSA algorithm for public-key cryptography. It defines the mathematical properties of public and private keys, primitive operations for encryption and signatures, secure cryptographic schemes, and related ASN.1 syntax representations.

The current version is 2.2 (2012-10-27). Compared to 2.1 (2002-06-14), which was republished as RFC 3447, version 2.2 updates the list of allowed hashing algorithms to align them with FIPS 180-4, therefore adding SHA-224, SHA-512/224 and SHA-512/256.

Keys

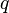The PKCS #1 standard defines the mathematical definitions and properties that RSA public and private keys must have. The traditional key pair is based on a modulus, n, that is the product of two distinct large prime numbers, p and q, such that n = pq.

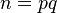Starting with version 2.1, this definition was generalized to allow for multi-prime keys, where the number of distinct primes may be two or more. When dealing with multi-prime keys, the prime factors are all generally labeled as r_i for some i, such that:

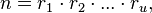n = r_1 \cdot r_2 \cdot ... \cdot r_u, for u \ge 2

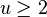
As a notational convenience, 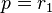p = r_1 and q = r_2.

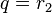The RSA public key is represented as the tuple 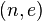(n, e), where the integer e is the public exponent.

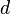The RSA private key may have two representations. The first compact form is the tuple (n, d), where d is the private exponent. The second form has at least five terms, or more for multi-prime keys. Although mathematically redundant to the compact form, the additional terms allow for certain computational optimizations when using the key.

Primitives

The standard defines several basic primitives. The primitive operations provide the fundamental instructions for turning the raw mathematical formulas into computable algorithms.

Schemes

By themselves the primitive operations do not necessarily provide any security. The concept of a cryptographic scheme is to define higher level algorithms or uses of the primitives so they achieve certain security goals.

There are two schemes for encryption and decryption:

There are also two schemes for dealing with signatures:

The two signature schemes make use of separately defined encoding methods:

The signature schemes are actually signatures with appendix, which means that rather than signing some input data directly, a hash function is used first to produce an intermediary representation of the data, and then the result of the hash is signed. This technique is almost always used with RSA because the amount of data that can be directly signed is proportional to the size of the keys; which is almost always much smaller than the amount of data an application may wish to sign.

Version history

External links

This article is issued from Wikipedia - version of the Saturday, February 21, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.