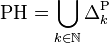PH (complexity)

In computational complexity theory, the complexity class PH is the union of all complexity classes in the polynomial hierarchy:

\mathrm{PH} = \bigcup_{k\in\mathbb{N}} \Delta_k^\mathrm{P}

PH was first defined by Larry Stockmeyer. It is a special case of hierarchy of bounded alternating Turing machine. It is contained in P^#P = P^PP (by Toda's theorem; the class of problems that are decidable by a polynomial time Turing machine with access to a #P or equivalently PP oracle), and also in PSPACE.

PH has a simple logical characterization: it is the set of languages expressible by second-order logic.

PH contains almost all well-known complexity classes inside PSPACE; in particular, it contains P, NP, and co-NP. It even contains probabilistic classes such as BPP and RP. However, there is some evidence that BQP, the class of problems solvable in polynomial time by a quantum computer, is not contained in PH (Aaronson 2010).

P = NP if and only if P = PH. This may simplify a potential proof of P ≠ NP, since it is only necessary to separate P from the more general class PH.

References

Bürgisser, Peter (2000). Completeness and reduction in algebraic complexity theory. Algorithms and Computation in Mathematics 7. Berlin: Springer-Verlag. p. 66. ISBN 3-540-66752-0. Zbl 0948.68082.
Stockmeyer, Larry J. (1977). "The polynomial-time hierarchy". Theor. Comput. Sci. 3: 1–22. doi:10.1016/0304-3975(76)90061-X. Zbl 0353.02024.
Scott Aaronson, BQP and the Polynomial Hierarchy, ACM STOC (2010), arXiv:0910.4698, ECCC TR09-104.
Complexity Zoo: PH

Important complexity classes (more)

Considered feasible	DLOGTIME AC⁰ ACC⁰ TC⁰ L SL RL NL NC SC CC P P-complete ZPP RP BPP BQP APX

Suspected infeasible	UP NP NP-complete NP-hard co-NP co-NP-complete AM QMA PH ⊕P PP #P #P-complete IP PSPACE PSPACE-complete

Considered infeasible	EXPTIME NEXPTIME EXPSPACE ELEMENTARY PR R RE ALL

Class hierarchies	Polynomial hierarchy Exponential hierarchy Grzegorczyk hierarchy Arithmetical hierarchy Boolean hierarchy

Families of classes	DTIME NTIME DSPACE NSPACE Probabilistically checkable proof Interactive proof system

This article is issued from Wikipedia - version of the Thursday, December 03, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.