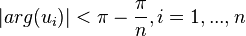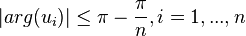P-matrix
In mathematics, a  -matrix is a complex square matrix with every principal minor > 0. A closely related class is that of
-matrix is a complex square matrix with every principal minor > 0. A closely related class is that of 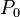 -matrices, which are the closure of the class of
-matrices, which are the closure of the class of  -matrices, with every principal minor
-matrices, with every principal minor 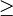 0.
0.
Spectra of  -matrices
-matrices
By a theorem of Kellogg,[1][2] the eigenvalues of  - and
- and 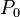 - matrices are bounded away from a wedge about the negative real axis as follows:
- matrices are bounded away from a wedge about the negative real axis as follows:
- If
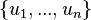 are the eigenvalues of an
are the eigenvalues of an  -dimensional
-dimensional  -matrix, then
-matrix, then
- If
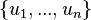 ,
, 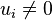 ,
, 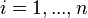 are the eigenvalues of an
are the eigenvalues of an  -dimensional
-dimensional 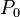 -matrix, then
-matrix, then
Remarks
The class of nonsingular M-matrices is a subset of the class of  -matrices. More precisely, all matrices that are both
-matrices. More precisely, all matrices that are both  -matrices and Z-matrices are nonsingular
-matrices and Z-matrices are nonsingular  -matrices. The class of sufficient matrices is another generalization of
-matrices. The class of sufficient matrices is another generalization of  -matrices.[3]
-matrices.[3]
The linear complementarity problem 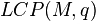 has a unique solution for every vector
has a unique solution for every vector 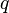 if and only if
if and only if  is a
is a  -matrix.[4]
-matrix.[4]
If the Jacobian of a function is a  -matrix, then the function is injective on any rectangular region of
-matrix, then the function is injective on any rectangular region of 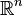 .[5]
.[5]
A related class of interest, particularly with reference to stability, is that of 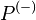 -matrices, sometimes also referred to as
-matrices, sometimes also referred to as 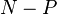 -matrices. A matrix
-matrices. A matrix  is a
is a 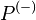 -matrix if and only if
-matrix if and only if 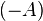 is a
is a  -matrix (similarly for
-matrix (similarly for 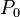 -matrices). Since
-matrices). Since 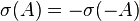 , the eigenvalues of these matrices are bounded away from the positive real axis.
, the eigenvalues of these matrices are bounded away from the positive real axis.
See also
- Q-matrix
- Z-matrix (mathematics)
- M-matrix
- Perron–Frobenius theorem
- Hurwitz matrix
- Linear complementarity problem
Notes
- ↑ Kellogg, R. B. (April 1972). "On complex eigenvalues ofM andP matrices". Numerische Mathematik 19 (2): 170–175. doi:10.1007/BF01402527.
- ↑ Fang, Li (July 1989). "On the spectra of P- and P0-matrices". Linear Algebra and its Applications 119: 1–25. doi:10.1016/0024-3795(89)90065-7.
- ↑ Csizmadia, Zsolt; Illés, Tibor (2006). "New criss-cross type algorithms for linear complementarity problems with sufficient matrices" (pdf). Optimization Methods and Software 21 (2): 247–266. doi:10.1080/10556780500095009. MR 2195759.
- ↑ Murty, Katta G. (January 1972). "On the number of solutions to the complementarity problem and spanning properties of complementary cones". Linear Algebra and its Applications 5 (1): 65–108. doi:10.1016/0024-3795(72)90019-5.
- ↑ Gale, David; Nikaido, Hukukane (10 December 2013). "The Jacobian matrix and global univalence of mappings". Mathematische Annalen 159 (2): 81–93. doi:10.1007/BF01360282.
References
- Csizmadia, Zsolt; Illés, Tibor (2006). "New criss-cross type algorithms for linear complementarity problems with sufficient matrices" (pdf). Optimization Methods and Software 21 (2): 247–266. doi:10.1080/10556780500095009. MR 2195759.
- David Gale and Hukukane Nikaido, The Jacobian matrix and global univalence of mappings, Math. Ann. 159:81-93 (1965) doi:10.1007/BF01360282
- Li Fang, On the Spectra of
 - and
- and 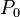 -Matrices, Linear Algebra and its Applications 119:1-25 (1989)
-Matrices, Linear Algebra and its Applications 119:1-25 (1989) - R. B. Kellogg, On complex eigenvalues of
 and
and  matrices, Numer. Math. 19:170-175 (1972)
matrices, Numer. Math. 19:170-175 (1972)