Osculating curve
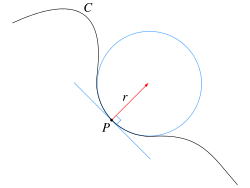
In differential geometry, an osculating curve is a plane curve from a given family that has the highest possible order of contact with another curve. That is, if F is a family of smooth curves, C is a smooth curve (not in general belonging to F), and p is a point on C, then an osculating curve from F at p is a curve from F that passes through p and has as many of its derivatives at p equal to the derivatives of C as possible.[1][2]
The term derives from the Latinate root "osculate", to kiss, because the two curves contact one another in a more intimate way than simple tangency.[3]
Examples
Examples of osculating curves of different orders include:
- The tangent line to a curve C at a point p, the osculating curve from the family of straight lines. The tangent line shares its first derivative (slope) with C and therefore has first-order contact with C.[1][2][4]
- The osculating circle to C at p, the osculating curve from the family of circles. The osculating circle shares both its first and second derivatives (equivalently, its slope and curvature) with C.[1][2][4]
- The osculating parabola to C at p, the osculating curve from the family of parabolas, has third order contact with C.[2][4]
- The osculating conic to C at p, the osculating curve from the family of conic sections, has fourth order contact with C.[2][4]
Generalizations
The concept of osculation can be generalized to higher-dimensional spaces, and to objects that are not curves within those spaces. For instance an osculating plane to a space curve is a plane that has second-order contact with the curve. This is as high an order as is possible in the general case.[5]
See also
References
- 1 2 3 Rutter, J. W. (2000), Geometry of Curves, CRC Press, pp. 174–175, ISBN 9781584881667.
- 1 2 3 4 5 Williamson, Benjamin (1912), An elementary treatise on the differential calculus: containing the theory of plane curves, with numerous examples, Longmans, Green, p. 309.
- ↑ Max, Black (1954–1955), "Metaphor", Proceedings of the Aristotelian Society, N.S. 55: 273–294. Reprinted in Johnson, Mark, ed. (1981), Philosophical Perspectives on Metaphor, University of Minnesota Press, pp. 63–82, ISBN 9780816657971. P. 69: "Osculating curves don't kiss for long, and quickly revert to a more prosaic mathematical contact."
- 1 2 3 4 Taylor, James Morford (1898), Elements of the Differential and Integral Calculus: With Examples and Applications, Ginn & Company, pp. 109–110.
- ↑ Kreyszig, Erwin (1991), Differential Geometry, Toronto University Mathematical Expositions 11, Courier Dover Publications, pp. 32–33, ISBN 9780486667218.