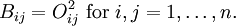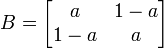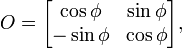Orthostochastic matrix

In mathematics, an orthostochastic matrix is a doubly stochastic matrix whose entries are the squares of the absolute values of the entries of some orthogonal matrix.

The detailed definition is as follows. A square matrix B of size n is doubly stochastic (or bistochastic) if all its rows and columns sum to 1 and all its entries are nonnegative real numbers, each of whose rows and columns sums to 1. It is orthostochastic if there exists an orthogonal matrix O such that

B_{ij}=O_{ij}^2 \text{ for } i,j=1,\dots,n. \,

All 2-by-2 doubly stochastic matrices are orthostochastic (and also unistochastic) since for any

B= \begin{bmatrix} a & 1-a \\ 1-a & a \end{bmatrix}

we find the corresponding orthogonal matrix

O = \begin{bmatrix} \cos \phi & \sin \phi \\ - \sin \phi & \cos \phi \end{bmatrix},

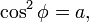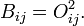
with $\cos^2 \phi =a,$ such that $B_{ij}=O_{ij}^2 .$

For larger n the sets of bistochastic matrices includes the set of unistochastic matrices, which includes the set of orthostochastic matrices and these inclusion relations are proper.

References

Brualdi, Richard A. (2006). Combinatorial matrix classes. Encyclopedia of Mathematics and Its Applications 108. Cambridge: Cambridge University Press. ISBN 0-521-86565-4. Zbl 1106.05001.

This article is issued from Wikipedia - version of the Sunday, March 08, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.