Order unit

An order unit is an element of an ordered vector space which can be used to bound all elements from above.^[1] In this way (as seen in the first example below) the order unit generalizes the unit element in the reals.

Definition

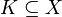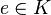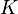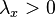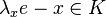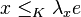For the ordering cone $K \subseteq X$ in the vector space $X$ , the element $e \in K$ is an order unit (more precisely an $K$ -order unit) if for every $x \in X$ there exists a $\lambda_x > 0$ such that $\lambda_x e - x \in K$ (i.e. $x \leq_K \lambda_x e$ ).^[2]

Equivalent definition

The order units of an ordering cone 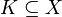$K \subseteq X$ are those elements in the algebraic interior of 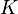$K$ , i.e. given by 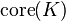$\operatorname{core}(K)$ .^[2]

Examples

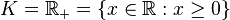Let $X = \mathbb{R}$ be the real numbers and $K = \mathbb{R}_+ = \{x \in \mathbb{R}: x \geq 0\}$ , then the unit element 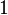$1$ is an order unit.

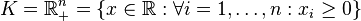Let $X = \mathbb{R}^n$ and $K = \mathbb{R}^n_+ = \{x \in \mathbb{R}: \forall i = 1,\ldots,n: x_i \geq 0\}$ , then the unit element 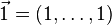$\vec{1} = (1,\ldots,1)$ is an order unit.

References

↑ Fuchssteiner, Benno; Lusky, Wolfgang (1981). Convex Cones. Elsevier. ISBN 9780444862907.
1 2 Charalambos D. Aliprantis; Rabee Tourky (2007). Cones and Duality. American Mathematical Society. ISBN 9780821841464.

This article is issued from Wikipedia - version of the Wednesday, December 26, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.