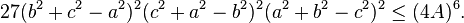Ono's inequality

In mathematics, Ono's inequality is a theorem about triangles in the Euclidean plane. In its original form, as conjectured by T. Ono in 1914, the inequality is actually false; however, the statement is true for acute triangles and right triangles, as shown by Balitrand in 1916.

Statement of the inequality

Consider an acute or right triangle in the Euclidean plane with side lengths a, b and c and area A. Then

27 (b^2 + c^2 - a^2)^2 (c^2 + a^2 - b^2)^2 (a^2 + b^2 - c^2)^2 \leq (4 A)^6.

This inequality fails for general triangles (to which Ono's original conjecture applied), as shown by the counterexample 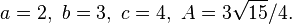$a=2, \, \, b=3, \, \, c=4, \, \, A=3\sqrt{15}/4.$

The inequality holds with equality in the case of an equilateral triangle, in which up to similarity we have sides 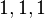$1,1,1$ and area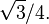 $\sqrt{3}/4.$

References

Balitrand, F. (1916). "Problem 4417". Intermed. Math. 23: 86–87.
Ono, T. (1914). "Problem 4417". Intermed. Math. 21: 146.
Quijano, G. (1915). "Problem 4417". Intermed. Math. 22: 66.

External links

Weisstein, Eric W., "Ono inequality", MathWorld.

Disproved conjectures

Borsuk's Chinese hypothesis Euler's sum of powers Ganea Hauptvermutung Hirsch Mertens Ono's inequality Pólya Ragsdale Schoen–Yau Seifert Tait's Von Neumann Weyl–Berry

This article is issued from Wikipedia - version of the Monday, June 29, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Ono's inequality

Statement of the inequality

See also

References

External links