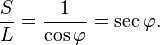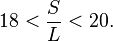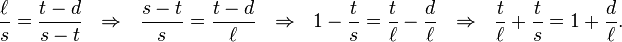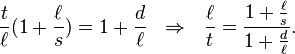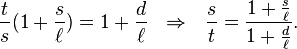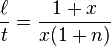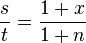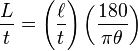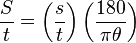On the Sizes and Distances (Aristarchus)

"On the Sizes and Distances" redirects here. For the work by Hipparchus, see On Sizes and Distances.
Aristarchus's 3rd century BC calculations on the relative sizes of, from left, the Sun, Earth and Moon, from a 10th-century CE Greek copy

On the Sizes and Distances (of the Sun and Moon) (Περὶ μεγεθῶν καὶ ἀποστημάτων [ἡλίου καὶ σελήνης], Peri megethon kai apostematon) is widely accepted as the only extant work written by Aristarchus of Samos, an ancient Greek astronomer who lived circa 310–230 BC. This work calculates the sizes of the Sun and Moon, as well as their distances from the Earth in terms of Earth's radius.

The book was presumably preserved by students of Pappus of Alexandria's course in mathematics, although we do not have the details of this. The editio princeps was published by John Wallis in 1688, using several medieval manuscripts compiled by Sir Henry Savile.[1] The earliest Latin translation was made by Georgio Valla in 1488. There is also a 1572 Latin translation and commentary by Frederico Commandino.[2][3]

Symbols

The work's method relied on several observations:

The rest of the article details a reconstruction of Aristarchus' method and results.[4] The reconstruction uses the following variables:

SymbolMeaning
φAngle between the Moon and the Sun during a half moon (directly measurable)
LDistance to the Moon
SDistance to the Sun
ℓRadius of the Moon
sRadius of the Sun
tRadius of the Earth
DDistance from the center of Earth to the vertex of Earth's shadow cone
dRadius of the Earth's shadow at the location of the Moon
nRatio, d/ℓ (a directly observable quantity during a lunar eclipse)
xRatio, S/L = s/ℓ (which is calculated from φ)

Half Moon

Aristarchus began with the premise that, during a half moon, the moon forms a right triangle with the Sun and Earth. By observing the angle between the Sun and Moon, φ, the ratio of the distances to the Sun and Moon could be deduced using a form of trigonometry.

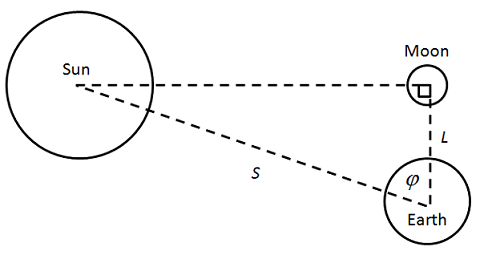
From the diagram and trigonometry, we can calculate that

\frac{S}{L} = \frac{1}{\cos \varphi} = \sec \varphi.

The diagram is greatly exaggerated, because in reality, S = 390 L, and φ is extremely close to 90°. Aristarchus determined φ to be a thirtieth of a quadrant (in modern terms, 3°) less than a right angle: in current terminology, 87°. Trigonometric functions had not yet been invented, but using geometrical analysis in the style of Euclid, Aristarchus determined that

18 < \frac{S}{L} < 20.

In other words, the distance to the Sun was somewhere between 18 and 20 times greater than the distance to the Moon. This value (or values close to it) was accepted by astronomers for the next two thousand years, until the invention of the telescope permitted a more precise estimate of solar parallax.

Aristarchus also reasoned that as the angular size of the Sun and the Moon were the same, but the distance to the Sun was between 18 and 20 times further than the Moon, the Sun must therefore be 18-20 times larger.

Lunar eclipse

Aristarchus then used another construction based on a lunar eclipse:

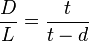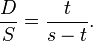
By similarity of the triangles, \frac{D}{L} = \frac{t}{t-d} \quad and \quad \frac{D}{S} = \frac{t}{s-t}.

Dividing these two equations and using the observation that the apparent sizes of the Sun and Moon are the same, 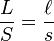\frac{L}{S} = \frac{\ell}{s}, yields

\frac{\ell}{s} = \frac{t-d}{s-t} \ \ \Rightarrow \ \ \frac{s-t}{s} = \frac{t-d}{\ell} \ \ \Rightarrow \ \ 1 - \frac{t}{s} = \frac{t}{\ell} - \frac{d}{\ell} \ \ \Rightarrow \ \ \frac{t}{\ell} + \frac{t}{s} = 1 + \frac{d}{\ell}.

The rightmost equation can either be solved for ℓ/t

\frac{t}{\ell}(1+\frac{\ell}{s}) = 1 + \frac{d}{\ell} \ \ \Rightarrow \ \ \frac{\ell}{t} = \frac{1+\frac{\ell}{s}}{1 + \frac{d}{\ell}}.

or s/t

\frac{t}{s}(1+\frac{s}{\ell}) = 1 + \frac{d}{\ell} \ \ \Rightarrow \ \ \frac{s}{t} = \frac{1+\frac{s}{\ell}}{1 + \frac{d}{\ell}}.

The appearance of these equations can be simplified using n = d/ℓ and x = s/ℓ.

\frac{\ell}{t} = \frac{1+x}{x(1+n)}
\frac{s}{t} = \frac{1+x}{1+n}

The above equations give the radii of the Moon and Sun entirely in terms of observable quantities.

The following formulae give the distances to the Sun and Moon in terrestrial units:

\frac{L}{t} = \left( \frac{\ell}{t} \right) \left( \frac{180}{\pi \theta} \right)
\frac{S}{t} = \left( \frac{s}{t} \right) \left( \frac{180}{\pi \theta} \right)

where θ is the apparent radius of the Moon and Sun measured in degrees.

It is unlikely that Aristarchus used these exact formulae, yet these formulae are likely a good approximation to those of Aristarchus.

Results

The above formulae can be used to reconstruct the results of Aristarchus. The following table shows the results of a long-standing (but dubious) reconstruction using n = 2, x = 19.1 (φ = 87°) and θ = 1°, alongside the modern day accepted values.

QuantityRelationReconstructionModern
s/tSun's radius in Earth radii6.7109
t/ℓEarth's radius in Moon radii2.853.50
L/tEarth-Moon distance in Earth radii2060.32
S/tEarth-Sun distance in Earth radii38023,500

The error in this calculation comes primarily from the poor values for x and θ. The poor value for θ is especially surprising, since Archimedes writes that Aristarchus was the first to determine that the Sun and Moon had an apparent diameter of half a degree. This would give a value of θ = 0.25, and a corresponding distance to the moon of 80 Earth radii, a much better estimate. The disagreement of the work with Archimedes seems to be due to its taking an Aristarchos statement that the lunisolar diameter is 1/15 of a "meros" of the zodiac to mean 1/15 of a zodiacal sign (30°), unaware that the Greek word "meros" meant either "portion" or 7°1/2; and 1/15 of the latter amount is 1°/2, in agreement with Archimedes' testimony.

A similar procedure was later used by Hipparchus, who estimated the mean distance to the moon as 67 Earth radii, and Ptolemy, who took 59 Earth radii for this value.

Illustrations

Some interactive illustrations of the propositions in On Sizes can be found here:

Notes

  1. ↑ Heath, Thomas (1913). Aristarchus of Samos, the Ancient Copernicus. Oxford: Clarendon. p. 323.
  2. ↑ Arch. Hist. Exact Sci. 61 (2007) 213–54.
  3. ↑ Noack B. (1992) Aristarch von Samos: Untersuchungen zur Überlieferungsgeschichte der Schrif Περὶ μεγεθῶν καὶ ἀποστημάτων ἡλίου καὶ σελήνης, Wiesbaden.
  4. ↑ A video on reconstruction of Aristarchus' method
  5. ↑ Berggren, J. L. & N. Sidoli (2007) ‘Aristarchus's On the Sizes and Distances of the Sun and the Moon: Greek and Arabic Texts’, Archive for History of Exact Sciences, Vol. 61, no. 3, 213-254 at the Wayback Machine (archived April 28, 2011).

Known copies

Works cited

This article is issued from Wikipedia - version of the Thursday, December 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.