Runcinated 120-cells
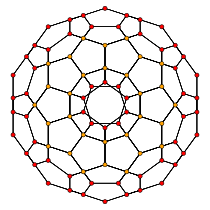 120-cell |
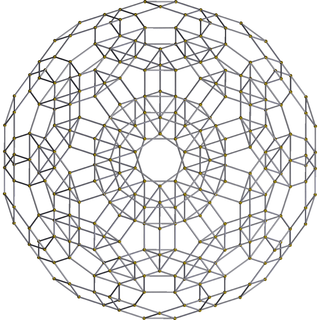 Runcinated 120-cell (Expanded 120-cell) |
 Runcitruncated 120-cell |
 600-cell |
 Runcitruncated 600-cell |
 Omnitruncated 120-cell |
| Orthogonal projections in H3 Coxeter plane | ||
|---|---|---|
In four-dimensional geometry, a runcinated 120-cell (or runcinated 600-cell) is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular 120-cell.
There are 4 degrees of runcinations of the 120-cell including with permutations truncations and cantellations.
The runcinated 120-cell can be seen as an expansion applied to a regular 4-polytope, the 120-cell or 600-cell.
Runcinated 120-cell
| Runcinated 120-cell | |
|---|---|
| Type | Uniform 4-polytope |
| Uniform index | 38 |
| Coxeter diagram | |
| Cells | 2640 total: 120 5.5.5 720 4.4.5 1200 4.4.3 600 3.3.3 |
| Faces | 7440: 2400{3}+3600{4}+ 1440{5} |
| Edges | 7200 |
| Vertices | 2400 |
| Vertex figure |  Equilateral-triangular antipodium |
| Schläfli symbol | t0,3{5,3,3} |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex |
The runcinated 120-cell or small disprismatohexacosihecatonicosachoron is a uniform 4-polytope. It has 2640 cells: 120 dodecahedra, 720 pentagonal prisms, 1200 triangular prisms, and 600 tetrahedra. Its vertex figure is a nonuniform triangular antiprism (equilateral-triangular antipodium): its bases represent a dodecahedron and a tetrahedron, and its flanks represent three triangular prisms and three pentagonal prisms.
Alternate names
- Runcinated 120-cell / Runcinated 600-cell (Norman W. Johnson)
- Runcinated hecatonicosachoron / Runcinated dodecacontachoron / Runcinated hexacosichoron / Runcinated polydodecahedron / Runcinated polytetrahedron
- Small diprismatohexacosihecatonicosachoron (acronym: sidpixhi) (George Olshevsky, Jonathan Bowers)[1]
Images
 |
 H3 |
 A2/B3 |
 A3/B2 |
Runcitruncated 120-cell
| Runcitruncated 120-cell | |
|---|---|
| Type | Uniform 4-polytope |
| Uniform index | 43 |
| Coxeter diagram | |
| Cells | 2640 total: 120 (3.10.10) |
| Faces | 13440: 4800{3}+7200{4}+ 1440{10} |
| Edges | 18000 |
| Vertices | 7200 |
| Vertex figure |  Irregular rectangular pyramid |
| Schläfli symbol | t0,1,3{5,3,3} |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex |
The runcitruncated 120-cell or prismatorhombated hexacosichoron is a uniform 4-polytope. It contains 2640 cells: 120 truncated dodecahedra, 720 decagonal prisms, 1200 triangular prisms, and 600 cuboctahedra. Its vertex figure is an irregular rectangular pyramid, with one truncated dodecahedron, two decagonal prisms, one triangular prism, and one cuboctahedron.
Alternate names
- Runcicantellated 600-cell (Norman W. Johnson)
- Prismatorhombated hexacosichoron (Acronym: prix) (George Olshevsky, Jonathan Bowers)[2]
Images
 |
 H3 |
 A2/B3 |
 A3/B2 |
Runcitruncated 600-cell
| Runcitruncated 600-cell | |
|---|---|
| Type | Uniform 4-polytope |
| Uniform index | 44 |
| Coxeter diagram | |
| Cells | 2640 total: 120 3.4.5.4 720 4.4.5 1200 4.4.6 600 3.6.6 |
| Faces | 13440: 2400{3}+7200{4}+ 1440{5}+2400{6} |
| Edges | 18000 |
| Vertices | 7200 |
| Vertex figure |  Trapezoidal pyramid |
| Schläfli symbol | t0,1,3{3,3,5} |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex |
The runcitruncated 600-cell or prismatorhombated hecatonicosachoron is a uniform 4-polytope. It is composed of 2640 cells: 120 rhombicosidodecahedron, 600 truncated tetrahedra, 720 pentagonal prisms, and 1200 hexagonal prisms. It has 7200 vertices, 18000 edges, and 13440 faces (2400 triangles, 7200 squares, and 2400 hexagons).
Alternate names
- Runcicantellated 120-cell (Norman W. Johnson)
- Prismatorhombated hecatonicosachoron (Acronym: prahi) (George Olshevsky, Jonathan Bowers)[3]
Images
 |
 H3 |
 A2/B3 |
 A3/B2 |
Omnitruncated 120-cell
| Omnitruncated 120-cell | |
|---|---|
| Type | Uniform 4-polytope |
| Uniform index | 46 |
| Coxeter diagram | |
| Cells | 2640 total: 120 4.6.10 720 4.4.10 1200 4.4.6 600 4.6.6 |
| Faces | 17040 total: 10800 {4}, 4800 {6} 1440 {10} |
| Edges | 28800 |
| Vertices | 14400 |
| Vertex figure |  Chiral scalene tetrahedron |
| Schläfli symbol | t0,1,2,3{3,3,5} |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex |
The omnitruncated 120-cell or great disprismatohexacosihecatonicosachoron is a convex uniform 4-polytope, composed of 2640 cells: 120 truncated icosidodecahedra, 600 truncated octahedra, 720 decagonal prisms, and 1200 hexagonal prisms. It has 14400 vertices, 28800 edges, and 17040 faces (10800 squares, 4800 hexagons, and 1440 decagons). It is the largest nonprismatic convex uniform 4-polytope.
The vertices and edges form the Cayley graph of the Coxeter group H4.
Alternate names
- Omnitruncated 120-cell / Omnitruncated 600-cell (Norman W. Johnson)
- Omnitruncated hecatonicosachoron / Omnitruncated hexacosichoron / Omnitruncated polydodecahedron / Omnitruncated polytetrahedron
- Great diprismatohexacosihecatonicosachoron (Acronym gidpixhi) (George Olshevsky, Jonathan Bowers)[4]
Images
 |
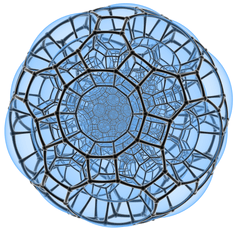 |
| Schlegel diagram (centered on truncated icosidodecahedron) (Orthogonal view, centered on decagonal prism cell.) |
Stereographic projection (centered on truncated icosidodecahedron) |
|---|
 H3 |
 A2/B3 |
 A3/B2 |
 Omnitruncated 120-cell |
 Dual to omnitruncated 120-cell |
Models
The first complete physical model of a 3D projection of the omnitruncated 120-cell was built by a team led by Daniel Duddy and David Richter on August 9, 2006 using the Zome system in the London Knowledge Lab for the 2006 Bridges Conference.[5]
Full snub 120-cell

The full snub 120-cell or omnisnub 120-cell, defined as an alternation of the omnitruncated 120-cell, can not be made uniform, but it can be given Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() , and symmetry [5,3,3]+, and constructed from 1200 octahedrons, 600 icosahedrons, 720 pentagonal antiprisms, 120 snub dodecahedrons, and 7200 tetrahedrons filling the gaps at the deleted vertices. It has 9840 cells, 35040 faces, 32400 edges, and 7200 vertices.[6]
, and symmetry [5,3,3]+, and constructed from 1200 octahedrons, 600 icosahedrons, 720 pentagonal antiprisms, 120 snub dodecahedrons, and 7200 tetrahedrons filling the gaps at the deleted vertices. It has 9840 cells, 35040 faces, 32400 edges, and 7200 vertices.[6]
Related polytopes
These polytopes are a part of a set of 15 uniform 4-polytopes with H4 symmetry:
| 120-cell | rectified 120-cell |
truncated 120-cell |
cantellated 120-cell |
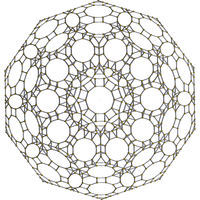
runcinated 120-cell |
cantitruncated 120-cell |
runcitruncated 120-cell |
omnitruncated 120-cell |
|---|---|---|---|---|---|---|---|
| {5,3,3} | r{5,3,3} | t{5,3,3} | rr{5,3,3} | t0,3{5,3,3} | tr{5,3,3} | t0,1,3{5,3,3} | t0,1,2,3{5,3,3} |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| 600-cell | rectified 600-cell |
truncated 600-cell |
cantellated 600-cell |
bitruncated 600-cell |
cantitruncated 600-cell |
runcitruncated 600-cell |
omnitruncated 600-cell |
| {3,3,5} | r{3,3,5} | t{3,3,5} | rr{3,3,5} | 2t{3,3,5} | tr{3,3,5} | t0,1,3{3,3,5} | t0,1,2,3{3,3,5} |
Notes
- ↑ Klitizing, (x3o3o5x - sidpixhi)
- ↑ Klitizing, (x3o3x5x - prix)
- ↑ Klitizing, (x3x3o5x - prahi)
- ↑ Klitizing, (x3x3x5x - gidpixhi)
- ↑ Photos of Zome model of omnitruncated 120/600-cell
- ↑ http://www.bendwavy.org/klitzing/incmats/s3s3s5s.htm
References
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation m55 m62 m60 m64
- Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 38, 44, 47, George Olshevsky.
- Richard Klitzing, 4D, uniform polytopes (polychora) x3o3o5x - sidpixhi, x3o3x5x - prix, x3x3o5x - prahi, x3x3x5x - gidpixhi
External links
- H4 uniform polytopes with coordinates: t03{5,3,3} t013{3,3,5} t013{5,3,3} t0123{5,3,3}
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||


