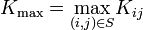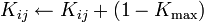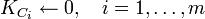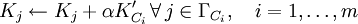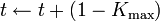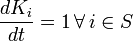Olami–Feder–Christensen model
In physics, in the area of dynamical systems, the Olami–Feder–Christensen model is an earthquake model conjectured to be an example of self-organized criticality where local exchange dynamics are not conservative. Despite the original claims of the authors and subsequent claims of other authors such as Lise, whether or not the model is self organized critical remains an open question.
The system behaviour reproduces some empirical laws that earthquakes follow (such as the Gutenberg–Richter law and Omori's Law)
Model definition
The model is a simplification of the Burridge-Knopoff model, where the blocks move instantly to their balanced positions when submitted to a force greater than their friction.
Let S be a square lattice with L × L sites and let Kmn ≥ 0 be the tension at site (m,n). The sites with tension greater than 1 are called critical and go through a relaxation step where their tension spreads to their neighbours. Through analogy with the Burridge-Knopoff model, what is being simulated is a fault, where one of the lattice's dimensions is the flaw depth and the other one follows the flaw.
Model rules
If there are no critical sites, then the system suffers a continuous drive, until a site becomes critical:
else if the sites C1, C2, ..., Cm are critical the relaxation rule is applied in parallel:
where K'C is the tension prior to the relaxation and ΓC is the set of neightbours of site C. α is called the conservative parameter and can range from 0 to 0.25 in a square lattice. This can create a chain reaction which is interpreted as an earthquake.
These rules allow us to define a time variable that is update during the driving step
this is equivalent to define a constant drive
and assume the relaxation step is instantaneous, which is a good approximation for an earthquake model.
Behaviour and criticality
The system's behaviour is heavily influenced by the α parameter. For α=0.25 the system is conservative (in the sense that the local exchange is conservative, as there is still tension loss in the borders) and clearly critical. For values α<0.25 the dynamics is very different, even in the limit α → 0.25, with greater noise and much greater transients. For low α, there are less possibilities of chain reactions which could lead to cut-offs in the earthquake size distribution, implying the model is not critical. Also, for α = 0, the model is trivially not critical.
These observations lead to the question of what is the value αc where the system makes the transition from critical to non-critical behaviour, which is still an open question.
References
- Christensen, K. and Olami, Z. (1992). "Variation of the Gutenberg-Richter
values and nontrivial temporal correlations in a spring-block model for earthquakes". Journal of Geophysical Research B 97: 8729–8735. Bibcode:1992JGR....97.8729C. doi:10.1029/92JB00427.
- Grassberger, P. (1994). "Efficient large-scale simulations of a uniformly driven system". Physical Review E 49: 2436–2444. Bibcode:1994PhRvE..49.2436G. doi:10.1103/PhysRevE.49.2436.
- Lise, S. and Paczuski, M. (2001). "Self-organized criticality and universality in a nonconservative earthquake model". Physical Review E 63: 036111. arXiv:cond-mat/0008010. Bibcode:2001PhRvE..63c6111L. doi:10.1103/PhysRevE.63.036111.
- Lise, S. and Paczuski, M. (2001). "Scaling in a nonconservative earthquake model of self-organized criticality". Physical Review E 64: 046111. arXiv:cond-mat/0104032. Bibcode:2001PhRvE..64d6111L. doi:10.1103/PhysRevE.64.046111.
- Olami, Z., Feder, H. J. S. and Christensen, K. (1992). "Self-organized criticality in a continuous, nonconservative cellular automaton modeling earthquakes". Physical Review Letters 68: 1244–1247. Bibcode:1992PhRvL..68.1244O. doi:10.1103/PhysRevLett.68.1244. PMID 10046116.