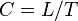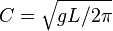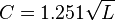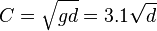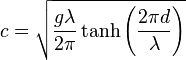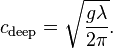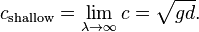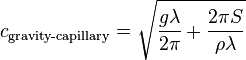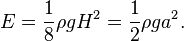Wind wave

Hurricane Marie storm waves

Video of large waves from Hurricane Marie along the coast of Newport Beach CA.

Ocean waves

The image shows the global distribution of wind speed and wave height as observed by NASA's TOPEX/Poseidon's dual-frequency radar altimeter from October 3 to October 12, 1992. Simultaneous observations of wind speed and wave height are helping scientists to predict ocean waves. Wind speed is determined by the strength of the radar signal after it has bounced off the ocean surface and returned to the satellite. A calm sea serves as a good reflector and returns a strong signal; a rough sea tends to scatter the signals and returns a weak pulse. Wave height is determined by the shape of the return radar pulse. A calm sea with low waves returns a condensed pulse whereas a rough sea with high waves returns a stretched pulse. Comparing the two images above shows a high degree of correlation between wind speed and wave height. The strongest winds (33.6 mph; 54.1 km/h) and highest waves are found in the Southern Ocean. The weakest winds—shown as areas of magenta and dark blue—are generally found in the tropical Oceans.

In fluid dynamics, wind waves, or wind-generated waves, are surface waves that occur on the free surface of oceans, seas, lakes, rivers, and canals or even on small puddles and ponds. They result from the wind blowing over an area of fluid surface. Waves in the oceans can travel thousands of miles before reaching land. Wind waves range in size from small ripples, to waves over 100 ft (30 m) high.^[1]

When directly generated and affected by local winds, a wind wave system is called a wind sea. After the wind ceases to blow, wind waves are called swells. More generally, a swell consists of wind-generated waves that are not significantly affected by the local wind at that time. They have been generated elsewhere or some time ago.^[2] Wind waves in the ocean are called ocean surface waves.

Wind waves have a certain amount of randomness: subsequent waves differ in height, duration, and shape with limited predictability. They can be described as a stochastic process, in combination with the physics governing their generation, growth, propagation and decay—as well as governing the interdependence between flow quantities such as: the water surface movements, flow velocities and water pressure. The key statistics of wind waves (both seas and swells) in evolving sea states can be predicted with wind wave models.

Although waves are usually considered in the water seas of Earth, the hydrocarbon seas of Titan may also have wind-driven waves.^[3]

Wave formation

NOAA ship Delaware II in bad weather on Georges Bank.

The great majority of large breakers seen on a beach result from distant winds. Five factors influence the formation of the flow structures in wind waves:^[4]

• Wind speed or strength relative to wave speed- the wind must be moving faster than the wave crest for energy transfer
• The uninterrupted distance of open water over which the wind blows without significant change in direction (called the fetch)
• Width of area affected by fetch
• Wind duration - the time over which the wind has blown over a given area
• Water depth

All of these factors work together to determine the size of wind waves and the structures of the flows within:

• Wave height (from high trough to crest)
• Wave length (from crest to crest)
• Wave period (time interval between arrival of consecutive crests at a stationary point)
• Wave propagation direction

water particles movements of deep a water wave.

A fully developed sea has the maximum wave size theoretically possible for a wind of a specific strength, duration, and fetch. Further exposure to that specific wind could only cause a loss of energy due to the breaking of wave tops and formation of "whitecaps". Waves in a given area typically have a range of heights. For weather reporting and for scientific analysis of wind wave statistics, their characteristic height over a period of time is usually expressed as significant wave height. This figure represents an average height of the highest one-third of the waves in a given time period (usually chosen somewhere in the range from 20 minutes to twelve hours), or in a specific wave or storm system. The significant wave height is also the value a "trained observer" (e.g. from a ship's crew) would estimate from visual observation of a sea state. Given the variability of wave height, the largest individual waves are likely to be somewhat less than twice the reported significant wave height for a particular day or storm.^[5]

The phases of an ocean surface wave: 1. Wave Crest, where the water masses of the surface layer are moving horizontally in the same direction as the propagating wave front. 2. Falling wave. 3. Trough, where the water masses of the surface layer are moving horizontally in the opposite direction of the wave front direction. 4. Rising wave.

• Sources of wind wave generation: Sea water wave is generated by many kinds of disturbances such as Seismic events, gravity, and crossing wind. The generation of wind wave is initiated by the disturbances of cross wind field on the surface of the sea water. Two major Mechanisms of surface wave formation by winds (a.k.a.‘The Miles-Phillips Mechanism’) and other sources (ex. earthquakes) of wave formation can explain the generation of wind waves.

However, if one set a flat water surface (Beaufort Point,0) and abrupt cross wind flows on the surface of the water, then the generation of surface wind waves can be explained by following two mechanisms which initiated by normal pressure fluctuations of turbulent winds and parallel wind shear flows.

• The mechanism of the surface wave generation by winds

the simple picture of the wave formation mechanism

1) Starts from "Fluctuations of wind" (O.M.Phillips) : the wind wave formation on water surface by wind is started by a random distribution of normal pressure acting on the water from the wind. By the mechanism developed by O.M. Phillips (in 1957), the water surface is initially at rest and wave generation is started by adding turbulent wind flows and then, by the fluctuations of the wind, normal pressure acting on the water surface. From this pressure fluctuation arise normal and tangential stresses to the surface water, which generates wave behavior on the water surface. It is assumed that:- ^[6]

1. The water originally at rest.
2. The water is not viscid.
3. The water is irrotational.
4. There are random distribution of normal pressure to the water surface from the turbulent wind.
5. Correlations between air and water motions are neglected.

2) starts from "wind shear forces" on the water surface (J.W.Miles, applied to mainly 2D deep water gravity waves) ; John W. Miles suggested a surface wave generation mechanism which is initiated by turbulent wind shear flows Ua(y), based on the inviscid Orr-Sommerfeld equation in 1957. He found the energy transfer from wind to water surface as a wave speed, c is proportional to the curvature of the velocity profile of wind Ua’’(y) at point where the mean wind speed is equal to the wave speed (Ua=c, where, Ua is the Mean turbulent wind speed). Since the wind profile Ua(y) is logarithmic to the water surface, the curvature Ua’’(y) have negative sign at the point of Ua=c. This relations show the wind flow transferring its kinetic energy to the water surface at their interface, and arises wave speed, c.

the growth-rate can be determined by the curvature of the winds ((d^2 Ua)/(dz^2 )) at the steering height (Ua (z=z_h)=c) for a given wind speed Ua {Assumptions; 1. 2D parallel shear flow, Ua(y) 2. incompressible, inviscid water / wind 3. irrotational water 4. slope of the displacement of surface is small}^[7]

Generally these wave formation mechanisms occur together on the ocean surface and arise wind waves and grows up to the fully developed waves.

For example,^[8]

If we suppose a very flat sea surface (Beaufort number, 0), and sudden wind flow blows steadily across the sea surface, physical wave generation process will be like;

1. Turbulent wind flows form random pressure fluctuations at the sea surface. Small waves with a few centimeters order of wavelengths is generated by the pressure fluctuations. (The Phillips mechanism^[6])

2. The cross wind keep acting on the initially fluctuated sea surface, then the wave become larger. As the wave become larger, the pressure differences get larger along to the wave growing, then the wave growth rate is getting faster. Then the shear instability expedites the wave growing exponentially. (The Miles mechanism^[6])

3. The interactions between the waves on the surface generate longer waves (Hasselmann et al., 1973^[9]) and the interaction will transfer wave energy from the shorter waves generated by the Miles mechanism to the waves have slightly lower frequencies than the frequency at the peak wave magnitudes, then finally the waves will be faster than the cross wind speed (Pierson & Moskowitz^[10]).

((NOTE: Most of the wave speeds calculated from the wave length divided by the period are proportional to sqrt (length). Thus, except for the shortest wave length, the waves follow the deep water theory described in the next section. The 28 ft long wave must be either in shallow water or between deep and shallow.))

Types of wind waves

Classification of the spectrum of ocean waves according to wave period.^[11]

Surf on a rocky irregular bottom. Porto Covo, west coast of Portugal

Three different types of wind waves develop over time:

• Capillary waves, or ripples
• Seas
• Swells

Ripples appear on smooth water when the wind blows, but will die quickly if the wind stops. The restoring force that allows them to propagate is surface tension. Sea waves are larger-scale, often irregular motions that form under sustained winds. These waves tend to last much longer, even after the wind has died, and the restoring force that allows them to propagate is gravity. As waves propagate away from their area of origin, they naturally separate into groups of common direction and wavelength. The sets of waves formed in this way are known as swells.

Individual "rogue waves" (also called "freak waves", "monster waves", "killer waves", and "king waves") much higher than the other waves in the sea state can occur. In the case of the Draupner wave, its 25 m (82 ft) height was 2.2 times the significant wave height. Such waves are distinct from tides, caused by the Moon and Sun's gravitational pull, tsunamis that are caused by underwater earthquakes or landslides, and waves generated by underwater explosions or the fall of meteorites—all having far longer wavelengths than wind waves.

Yet, the largest ever recorded wind waves are common — not rogue — waves in extreme sea states. For example: 29.1 m (95 ft) high waves have been recorded on the RRS Discovery in a sea with 18.5 m (61 ft) significant wave height, so the highest wave is only 1.6 times the significant wave height.^[12] The biggest recorded by a buoy (as of 2011) was 32.3 m (106 ft) high during the 2007 typhoon Krosa near Taiwan.^[13]

Ocean waves can be classified based on: the disturbing force(s) that create(s) them; the extent to which the disturbing force(s) continue(s) to influence them after formation; the extent to which the restoring force(s) weaken(s) (or flatten) them; and their wavelength or period. Seismic Sea waves have a period of ~20 minutes, and speeds of 760 km/h (470 mph). Wind waves (deep-water waves) have a period of about 20 seconds.

The speed of all ocean waves is controlled by gravity, wavelength, and water depth. Most characteristics of ocean waves depend on the relationship between their wavelength and water depth. Wavelength determines the size of the orbits of water molecules within a wave, but water depth determines the shape of the orbits. The paths of water molecules in a wind wave are circular only when the wave is traveling in deep water. A wave cannot "feel" the bottom when it moves through water deeper than half its wavelength because too little wave energy is contained in the small circles below that depth. Waves moving through water deeper than half their wavelength are known as deep-water waves. On the other hand, the orbits of water molecules in waves moving through shallow water are flattened by the proximity of the sea surface bottom. Waves in water shallower than 1/20 their original wavelength are known as shallow-water waves. Transitional waves travel through water deeper than 1/20 their original wavelength but shallower than half their original wavelength.

In general, the longer the wavelength, the faster the wave energy will move through the water. For deep-water waves, this relationship is represented with the following formula:

where C is speed (celerity), L is wavelength, and T is time, or period (in seconds).

The speed of a deep-water wave may also be approximated by:

where g is the acceleration due to gravity, 9.8 meters (32 feet) per second squared. Because g and π (3.14) are constants, the equation can be reduced to:

when C is measured in meters per second and L in meters. Note that in both instances that wave speed is proportional to wavelength.

The speed of shallow-water waves is described by a different equation that may be written as:

where C is speed (in meters per second), g is the acceleration due to gravity, and d is the depth of the water (in meters). The period of a wave remains unchanged regardless of the depth of water through which it is moving. As deep-water waves enter the shallows and feel the bottom, however, their speed is reduced and their crests "bunch up," so their wavelength shortens.

Wave shoaling and refraction

As waves travel from deep to shallow water, their shape alters (wave height increases, speed decreases, and length decreases as wave orbits become asymmetrical). This process is called shoaling.

Wave refraction is the process by which wave crests realign themselves as a result of decreasing water depths. Varying depths along a wave crest cause the crest to travel at different phase speeds, with those parts of the wave in deeper water moving faster than those in shallow water. This process continues until the crests become (nearly) parallel to the depth contours. Rays—lines normal to wave crests between which a fixed amount of energy flux is contained—converge on local shallows and shoals. Therefore, the wave energy between rays is concentrated as they converge, with a resulting increase in wave height.

Because these effects are related to a spatial variation in the phase speed, and because the phase speed also changes with the ambient current – due to the Doppler shift – the same effects of refraction and altering wave height also occur due to current variations. In the case of meeting an adverse current the wave steepens, i.e. its wave height increases while the wave length decreases, similar to the shoaling when the water depth decreases.^[15]

Wave breaking

Big wave breaking

Breaking of a wave reaching the beach

Some waves undergo a phenomenon called "breaking". A breaking wave is one whose base can no longer support its top, causing it to collapse. A wave breaks when it runs into shallow water, or when two wave systems oppose and combine forces. When the slope, or steepness ratio, of a wave is too great, breaking is inevitable.

Individual waves in deep water break when the wave steepness—the ratio of the wave height H to the wavelength λ—exceeds about 0.07, so for H > 0.07 λ. In shallow water, with the water depth small compared to the wavelength, the individual waves break when their wave height H is larger than 0.8 times the water depth h, that is H > 0.8 h.^[16] Waves can also break if the wind grows strong enough to blow the crest off the base of the wave.

Three main types of breaking waves are identified by surfers or surf lifesavers. Their varying characteristics make them more or less suitable for surfing, and present different dangers.

• Spilling, or rolling: these are the safest waves on which to surf. They can be found in most areas with relatively flat shorelines. They are the most common type of shorebreak
• Plunging, or dumping: these break suddenly and can "dump" swimmers—pushing them to the bottom with great force. These are the preferred waves for experienced surfers. Strong offshore winds and long wave periods can cause dumpers. They are often found where there is a sudden rise in the sea floor, such as a reef or sandbar.
• Surging: these may never actually break as they approach the water's edge, as the water below them is very deep. They tend to form on steep shorelines. These waves can knock swimmers over and drag them back into deeper water.

Science of waves

Stokes drift in shallow water waves (Animation)

Wind waves are mechanical waves that propagate along the interface between water and air; the restoring force is provided by gravity, and so they are often referred to as surface gravity waves. As the wind blows, pressure and friction perturb the equilibrium of the water surface and transfer energy from the air to the water, forming waves. The initial formation of waves by the wind is described in the theory of Phillips from 1957, and the subsequent growth of the small waves has been modeled by Miles, also in 1957.^[17][18]

Stokes drift in a deeper water wave (Animation)

Photograph of the water particle orbits under a – progressive and periodic – surface gravity wave in a wave flume. The wave conditions are: mean water depth d = 2.50 ft (0.76 m), wave height H = 0.339 ft (0.103 m), wavelength λ = 6.42 ft (1.96 m), period T = 1.12 s.^[19]

In linear plane waves of one wavelength in deep water, parcels near the surface move not plainly up and down but in circular orbits: forward above and backward below (compared the wave propagation direction). As a result, the surface of the water forms not an exact sine wave, but more a trochoid with the sharper curves upwards—as modeled in trochoidal wave theory.

When waves propagate in shallow water, (where the depth is less than half the wavelength) the particle trajectories are compressed into ellipses.^[20][21]

In reality, for finite values of the wave amplitude (height), the particle paths do not form closed orbits; rather, after the passage of each crest, particles are displaced slightly from their previous positions, a phenomenon known as Stokes drift.^[22][23]

As the depth below the free surface increases, the radius of the circular motion decreases. At a depth equal to half the wavelength λ, the orbital movement has decayed to less than 5% of its value at the surface. The phase speed (also called the celerity) of a surface gravity wave is – for pure periodic wave motion of small-amplitude waves – well approximated by

where

c = phase speed;

λ = wavelength;

d = water depth;

g = acceleration due to gravity at the Earth's surface.

In deep water, where 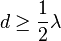, so 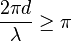and the hyperbolic tangent approaches 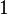, the speed approximates

In SI units, with 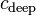in m/s, 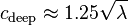, when is measured in metres. This expression tells us that waves of different wavelengths travel at different speeds. The fastest waves in a storm are the ones with the longest wavelength. As a result, after a storm, the first waves to arrive on the coast are the long-wavelength swells.

For intermediate and shallow water, the Boussinesq equations are applicable, combining frequency dispersion and nonlinear effects. And in very shallow water, the shallow water equations can be used.

If the wavelength is very long compared to the water depth, the phase speed (by taking the limit of c when the wavelength approaches infinity) can be approximated by

On the other hand, for very short wavelengths, surface tension plays an important role and the phase speed of these gravity-capillary waves can (in deep water) be approximated by

where

S = surface tension of the air-water interface;

= density of the water.^[24]

When several wave trains are present, as is always the case in nature, the waves form groups. In deep water the groups travel at a group velocity which is half of the phase speed.^[25] Following a single wave in a group one can see the wave appearing at the back of the group, growing and finally disappearing at the front of the group.

As the water depth 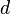decreases towards the coast, this will have an effect: wave height changes due to wave shoaling and refraction. As the wave height increases, the wave may become unstable when the crest of the wave moves faster than the trough. This causes surf, a breaking of the waves.

The movement of wind waves can be captured by wave energy devices. The energy density (per unit area) of regular sinusoidal waves depends on the water density , gravity acceleration and the wave height (which, for regular waves, is equal to twice the amplitude, ):

The velocity of propagation of this energy is the group velocity.

Wind wave models

Surfers are very interested in the wave forecasts. There are many websites that provide predictions of the surf quality for the upcoming days and weeks. Wind wave models are driven by more general weather models that predict the winds and pressures over the oceans, seas and lakes.

Wind wave models are also an important part of examining the impact of shore protection and beach nourishment proposals. For many beach areas there is only patchy information about the wave climate, therefore estimating the effect of wind waves is important for managing littoral environments.

Seismic signals

Ocean water waves generate land seismic waves that propagate hundreds of kilometers into the land.^[26] These seismic signals usually have the period of 6 ± 2 seconds. Such recordings were first reported and understood in about 1900.

There are two types of seismic "ocean waves". The primary waves are generated in shallow waters by direct water wave-land interaction and have the same period as the water waves (10 to 16 seconds). The more powerful secondary waves are generated by the superposition of ocean waves of equal period traveling in opposite directions, thus generating standing gravity waves – with an associated pressure oscillation at half the period, which is not diminishing with depth. The theory for microseism generation by standing waves was provided by Michael Longuet-Higgins in 1950, after in 1941 Pierre Bernard suggested this relation with standing waves on the basis of observations.^[27][28]

Internal waves

Internal waves can form at the boundary between water layers of different densities. These sub-surface waves are called internal waves. As is the case with ocean waves at the air-ocean interface, internal waves possess troughs, crests, wavelength, and period. Internal waves move very slowly because the density difference between the joined media is very small. Internal waves occur in the ocean at the base of the pycnocline, especially at the bottom edge of a steep thermocline. The wave height of internal waves may be greater than 30 meters (98 feet), causing the pycnocline to undulate slowly through a considerable depth. Their wavelength often exceeds 0.8 kilometres (0.50 mi) and their periods are typically 5 to 8 minutes. Internal waves are generated by wind energy, tidal energy, and ocean currents. Surface manifestations of internal waves have been photographed from space.

Internal waves may mix nutrients into surface water and trigger plankton blooms. They can also affect submarines and oil platforms.

See also

Notes

References

Scientific

• G.G. Stokes (1880). Mathematical and Physical Papers, Volume I. Cambridge University Press. pp. 197–229. 
• Phillips, O.M. (1977). The dynamics of the upper ocean (2nd ed.). Cambridge University Press. ISBN 0-521-29801-6. 
• Holthuijsen, Leo H. (2007). Waves in oceanic and coastal waters. Cambridge University Press. ISBN 0-521-86028-8. 
• Janssen, Peter (2004). The interaction of ocean waves and wind. Cambridge University Press. ISBN 978-0-521-46540-3. 

Other

• Rousmaniere, John (1989). The Annapolis Book of Seamanship (2nd revised ed.). Simon & Schuster. ISBN 0-671-67447-1. 
• Carr, Michael (October 1998). "Understanding Waves". Sail: 38–45. 

External links

Wikimedia Commons has media related to Ocean surface waves.

Wikimedia Commons has media related to Water waves.

• "Anatomy of a Wave" Holben, Jay boatsafe.com captured 5/23/06
• NOAA National Weather Service
• ESA press release on swell tracking with ASAR onboard ENVISAT
• Introductory oceanography chapter 10 – Ocean Waves
• HyperPhysics – Ocean Waves

Coastal geography Landforms Anchialine pool Archipelago Atoll Avulsion Ayre Barrier island Bay Baymouth bar Bight Bodden Brackish marsh Cape Channel Cliff Coast Coastal plain Coastal waterfall Continental margin Continental shelf Coral reef Cove Dune cliff-top Estuary Firth Fjard Fjord Freshwater marsh Fundus Gat Geo Gulf Gut Headland Inlet Intertidal wetland Island Islet Isthmus Lagoon Machair Marine terrace Mega delta Mouth bar Mudflat Natural arch Peninsula Reef Regressive delta Ria River delta Salt marsh Shoal Shore Skerry Sound Stack Strait Strand plain Submarine canyon Tidal island Tidal marsh Tide pool Tied island Tombolo Windwatt Beaches Beach cusps Beach evolution Beach morphodynamics Beach ridge Beachrock Pocket beach Raised beach Recession Shell beach Shingle beach Storm beach Wash margin Processes Blowhole Cliffed coast Coastal biogeomorphology Coastal erosion Concordant coastline Current Cuspate foreland Discordant coastline Emergent coastline Feeder bluff Fetch Flat coast Graded shoreline Headlands and bays Ingression coast Large-scale coastal behaviour Longshore drift Marine regression Marine transgression Raised shoreline Rip current Rocky shore Sea cave Sea foam Shoal Spit Steep coast Submergent coastline Surf break Surf zone Surge channel Swash Undertow Volcanic arc Wave-cut platform Wave shoaling Wind wave Wrack zone Management Accretion Coastal management Integrated coastal zone management Submersion Related Bulkhead line Grain size boulder clay cobble granule pebble sand shingle silt Intertidal zone Littoral zone Physical oceanography Region of freshwater influence Category Commons

Physical oceanography Waves Airy wave theory Ballantine scale Benjamin–Feir instability Boussinesq approximation Breaking wave Clapotis Cnoidal wave Cross sea Dispersion Edge wave Equatorial waves Fetch Gravity wave Infragravity wave Internal wave Kelvin wave Kinematic wave Longshore drift Luke's variational principle Mild-slope equation Radiation stress Rogue wave Rossby wave Rossby-gravity waves Sea state Seiche Significant wave height Sneaker wave Soliton Stokes boundary layer Stokes drift Stokes wave Swell Trochoidal wave Tsunami megatsunami Undertow Ursell number Wave action Wave base Wave height Wave power Wave radar Wave setup Wave shoaling Wave turbulence Wave–current interaction Waves and shallow water one-dimensional Saint-Venant equation shallow water equations Wind wave model Circulation Atmospheric circulation Baroclinity Boundary current Coriolis effect Downwelling Eddy Ekman layer Ekman spiral Ekman transport El Niño Southern Oscillation General Circulation Model Geostrophic current Global Ocean Data Analysis Project Gulf Stream Halothermal circulation Humboldt Current Hydrothermal circulation Langmuir circulation Longshore drift Loop Current Maelstrom Modular ocean model Ocean dynamics Ocean gyre Princeton ocean model Rip current Subsurface currents Sverdrup balance Thermohaline circulation shutdown Upwelling Whirlpool World Ocean Circulation Experiment Tides Amphidromic point Earth tide Head of tide Internal tide Lunitidal interval Perigean spring tide Rip tide Rule of twelfths Slack water Tidal bore Tidal force Tidal power Tidal race Tidal range Tidal resonance Tide gauge Tideline Landforms Abyssal fan Abyssal plain Atoll Bathymetric chart Coastal geography Cold seep Continental margin Continental rise Continental shelf Contourite Guyot Hydrography Oceanic basin Oceanic plateau Oceanic trench Passive margin Seabed Seamount Submarine canyon Plate tectonics Convergent boundary Divergent boundary Fracture zone Hydrothermal vent Marine geology Mid-ocean ridge Mohorovičić discontinuity Vine–Matthews–Morley hypothesis Oceanic crust Outer trench swell Ridge push Seafloor spreading Slab pull Slab suction Slab window Subduction Transform fault Volcanic arc Ocean zones Benthic Deep ocean water Deep sea Littoral Mesopelagic Oceanic Pelagic Photic Surf Sea level Deep-ocean Assessment and Reporting of Tsunamis Future sea level Global Sea Level Observing System North West Shelf Operational Oceanographic System Ocean Surface Topography Mission Sea-level curve Sea level rise World Geodetic System Acoustics Deep scattering layer Hydroacoustics Ocean acoustic tomography Sofar bomb SOFAR channel Underwater acoustics Related Argo Benthic lander Color of water DSV Alvin Marginal sea Marine energy Marine pollution Mooring National Oceanographic Data Center Ocean Ocean exploration Ocean observations Ocean reanalysis Ocean surface topography Ocean thermal energy conversion Oceanography Pelagic sediment Sea surface microlayer Sea surface temperature Seawater Science On a Sphere Thermocline Underwater glider Water column World Ocean Atlas Category Commons