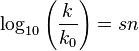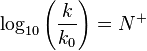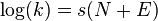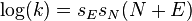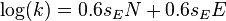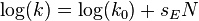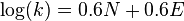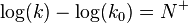Nucleophile

A nucleophile is a chemical species that donates an electron pair to an electrophile to form a chemical bond in relation to a reaction. All molecules or ions with a free pair of electrons or at least one pi bond can act as nucleophiles. Because nucleophiles donate electrons, they are by definition Lewis bases.

Nucleophilic describes the affinity of a nucleophile to the nuclei. Nucleophilicity, sometimes referred to as nucleophile strength, refers to a substance's nucleophilic character and is often used to compare the affinity of atoms.

Neutral nucleophilic reactions with solvents such as alcohols and water are named solvolysis. Nucleophiles may take part in nucleophilic substitution, whereby a nucleophile becomes attracted to a full or partial positive charge.

History

The terms nucleophile and electrophile were introduced by Christopher Kelk Ingold in 1933,^[1] replacing the terms anionoid and cationoid proposed earlier by A. J. Lapworth in 1925.^[2]

The word nucleophile is derived from nucleus and the Greek word φιλος, philos for love.

Properties

In general, in a row across the periodic table, the more basic the ion (the higher the pK_a of the conjugate acid) the more reactive it is as a nucleophile. In a given group, polarizability is more important in the determination of the nucleophilicity: The easier it is to distort the electron cloud around an atom or molecule the more readily it will react; e.g., the iodide ion (I⁻) is more nucleophilic than the fluoride ion (F⁻).

Nucleophilicity

Many schemes attempting to quantify relative nucleophilic strength have been devised. The following empirical data have been obtained by measuring reaction rates for a large number of reactions involving a large number of nucleophiles and electrophiles. Nucleophiles displaying the so-called alpha effect are usually omitted in this type of treatment.

Swain-Scott equation

The first such attempt is found in the Swain–Scott equation^[3][4] derived in 1953:

This free-energy relationship relates the pseudo first order reaction rate constant (in water at 25 °C), k, of a reaction, normalized to the reaction rate, k₀, of a standard reaction with water as the nucleophile, to a nucleophilic constant n for a given nucleophile and a substrate constant s that depends on the sensitivity of a substrate to nucleophilic attack (defined as 1 for methyl bromide).

This treatment results in the following values for typical nucleophilic anions: acetate 2.7, chloride 3.0, azide 4.0, hydroxide 4.2, aniline 4.5, iodide 5.0, and thiosulfate 6.4. Typical substrate constants are 0.66 for ethyl tosylate, 0.77 for β-propiolactone, 1.00 for 2,3-epoxypropanol, 0.87 for benzyl chloride, and 1.43 for benzoyl chloride.

The equation predicts that, in a nucleophilic displacement on benzyl chloride, the azide anion reacts 3000 times faster than water.

Ritchie equation

The Ritchie equation, derived in 1972, is another free-energy relationship:^[5][6][7]

where N⁺ is the nucleophile dependent parameter and k₀ the reaction rate constant for water. In this equation, a substrate-dependent parameter like s in the Swain–Scott equation is absent. The equation states that two nucleophiles react with the same relative reactivity regardless of the nature of the electrophile, which is in violation of the Reactivity–selectivity principle. For this reason this equation is also called the constant selectivity relationship.

In the original publication the data were obtained by reactions of selected nucleophiles with selected electrophilic carbocations such as tropylium or diazonium cations:

or (not displayed) ions based on Malachite green. Many other reaction types have since been described.

Typical Ritchie N⁺ values (in methanol) are: 0.5 for methanol, 5.9 for the cyanide anion, 7.5 for the methoxide anion, 8.5 for the azide anion, and 10.7 for the thiophenol anion. The values for the relative cation reactivities are -0.4 for the malachite green cation, +2.6 for the benzenediazonium cation, and +4.5 for the tropylium cation.

Mayr-Patz equation

In the Mayr-Patz equation (1994):^[8]

The second order reaction rate constant k at 20°C for a reaction is related to a nucleophilicity parameter N, an electrophilicity parameter E, and a nucleophile-dependent slope parameter s. The constant s is defined as 1 with 2-methyl-1-pentene as the nucleophile.

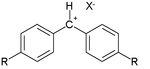
Many of the constants have been derived from reaction of so-called benzhydrylium ions as the electrophiles:^[9]

and a diverse collection of π-nucleophiles:

.

Typical E values are +6.2 for R = chlorine, +5.90 for R = hydrogen, 0 for R = methoxy and -7.02 for R = dimethylamine.

Typical N values with s in parenthesis are -4.47 (1.32) for electrophilic aromatic substitution to toluene (1), -0.41 (1.12) for electrophilic addition to 1-phenyl-2-propene (2), and 0.96 (1) for addition to 2-methyl-1-pentene (3), -0.13 (1.21) for reaction with triphenylallylsilane (4), 3.61 (1.11) for reaction with 2-methylfuran (5), +7.48 (0.89) for reaction with isobutenyltributylstannane (6) and +13.36 (0.81) for reaction with the enamine 7.^[10]

The range of organic reactions also include SN2 reactions:^[11]

With E = -9.15 for the S-methyldibenzothiophenium ion, typical nucleophile values N (s) are 15.63 (0.64) for piperidine, 10.49 (0.68) for methoxide, and 5.20 (0.89) for water. In short, nucleophilicities towards sp₂ or sp₃ centers follow the same pattern.

Unified equation

In an effort to unify the above described equations the Mayr equation is rewritten as:^[11]

with s_E the electrophile-dependent slope parameter and s_N the nucleophile-dependent slope parameter. This equation can be rewritten in several ways:

• with s_E = 1 for carbocations this equation is equal to the original Mayr-Patz equation of 1994,
• with s_N = 0.6 for most n nucleophiles the equation becomes

or the original Scott-Swain equation written as:

• with s_E = 1 for carbocations and s_N = 0.6 the equation becomes:

or the original Ritchie equation written as:

Types

Examples of nucleophiles are anions such as Cl⁻, or a compound with a lone pair of electrons such as NH₃ (ammonia).

In the example below, the oxygen of the hydroxide ion donates an electron pair to bond with the carbon at the end of the bromopropane molecule. The bond between the carbon and the bromine then undergoes heterolytic fission, with the bromine atom taking the donated electron and becoming the bromide ion (Br⁻), because a S_N2 reaction occurs by backside attack. This means that the hydroxide ion attacks the carbon atom from the other side, exactly opposite the bromine ion. Because of this backside attack, S_N2 reactions result in a reversal of the configuration of the electrophile. If the electrophile is chiral, it typically maintains its chirality, though the S_N2 product's configuration is flipped as compared to that of the original electrophile.

An ambident nucleophile is one that can attack from two or more places, resulting in two or more products. For example, the thiocyanate ion (SCN⁻) may attack from either the S or the N. For this reason, the S_N2 reaction of an alkyl halide with SCN⁻ often leads to a mixture of RSCN (an alkyl thiocyanate) and RNCS (an alkyl isothiocyanate). Similar considerations apply in the Kolbe nitrile synthesis.

Carbon

Carbon nucleophiles are alkyl metal halides found in the Grignard reaction, Blaise reaction, Reformatsky reaction, and Barbier reaction, organolithium reagents, and anions of a terminal alkyne.

Enols are also carbon nucleophiles. The formation of an enol is catalyzed by acid or base. Enols are ambident nucleophiles, but, in general, nucleophilic at the alpha carbon atom. Enols are commonly used in condensation reactions, including the Claisen condensation and the aldol condensation reactions.

Oxygen

Examples of oxygen nucleophiles are water (H₂O), hydroxide anion, alcohols, alkoxide anions, hydrogen peroxide, and carboxylate anions Nuclophilic attack does not take place during intermolecular hydrogen bonding.

Sulfur

Of sulfur nucleophiles, hydrogen sulfide and its salts, thiols (RSH), thiolate anions (RS⁻), anions of thiolcarboxylic acids (RC(O)-S⁻), and anions of dithiocarbonates (RO-C(S)-S⁻) and dithiocarbamates (R₂N-C(S)-S⁻) are used most often.

In general, sulfur is very nucleophilic because of its large size, which makes it readily polarizable, and its lone pairs of electrons are readily accessible.

Nitrogen

Nitrogen nucleophiles include ammonia, azide, amines, and nitrites.

See also

• Electrophile
• Lewis acids and bases
• Nucleophilic abstraction
• Addition to pi ligands

References