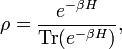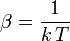Nuclear magnetic resonance quantum computer

Molecule of alanine used in NMR implementation of quantum computing. Qubits are implemented by spin states of the black carbon atoms

Nuclear Magnetic Resonance (NMR) quantum computing uses the spin states of molecules as qubits. NMR differs from other implementations of quantum computers in that it uses an ensemble of systems, in this case molecules. The ensemble is initialized to be the thermal equilibrium state (see quantum statistical mechanics). In mathematical parlance, this state is given by the density matrix:

\rho = \frac{e^{- \beta H}}{\operatorname{Tr}(e^{- \beta H})},

where H is the hamiltonian matrix of an individual molecule and

\beta = \frac{1}{k \, T}

where k is the Boltzmann constant and T the temperature.

Operations are performed on the ensemble through radio frequency (RF) pulses applied perpendicular to a strong, static field, created by a very large magnet. See nuclear magnetic resonance.

Some early success was obtained in performing quantum algorithms in NMR systems due to the relative maturity of NMR technology. For instance, in 2001 researchers at IBM reported the successful implementation of Shor's algorithm in a 7-qubit NMR quantum computer.[1]

However, even from the early days, it was recognized that NMR quantum computers would never be very useful due to the poor scaling of signal to noise in such systems.[2] More recent work, particularly by Caves and others, shows that all experiments in liquid state bulk ensemble NMR quantum computing to date do not possess quantum entanglement, thought to be required for quantum computation. Hence NMR quantum computing experiments are likely to have been only classical simulations of a quantum computer.[3]

References

  1. ↑ Vandersypen LMK, Steffen M, Breyta G, Yannoni CS, Sherwood MH, Chuang IL (2001). "Experimental realization of Shor's quantum factoring algorithm using nuclear magnetic resonance". Nature 414 (6866): 883–887. arXiv:quant-ph/0112176. Bibcode:2001Natur.414..883V. doi:10.1038/414883a. PMID 11780055.
  2. ↑ Warren WS (1997). "The usefulness of NMR quantum computing". Science 277 (5332): 1688–1689. doi:10.1126/science.277.5332.1688.
  3. ↑ Menicucci NC, Caves CM (2002). "Local realistic model for the dynamics of bulk-ensemble NMR information processing". Physical Review Letters 88 (16). arXiv:quant-ph/0111152. Bibcode:2002PhRvL..88p7901M. doi:10.1103/PhysRevLett.88.167901.
This article is issued from Wikipedia - version of the Monday, October 12, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.