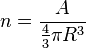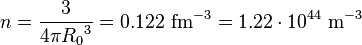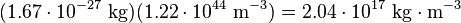Nuclear density
Nuclear density is the density of the nucleus of an atom, averaging about 2.3×1017 kg/m3. The descriptive term nuclear density is also applied to situations where similarly high densities occur, such as within neutron stars.
The nuclear density for a typical nucleus can be approximately calculated from the size of the nucleus, which itself can be approximated based on the number of protons and neutrons in it. The radius of a typical nucleus, in terms of number of nucleons, is
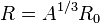 where
where  is the mass number and
is the mass number and 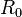 is 1.25 fm, with deviations of 0.2 fm from this value. The density of the nucleus is thus:
is 1.25 fm, with deviations of 0.2 fm from this value. The density of the nucleus is thus:
The mass density is the product of n by the nuclear mass.
For a single nucleon, A=1, therefore
The experimentally determined value for n is 0.16 fm−3. The calculated mass density, using a nucleon mass of 1.67×10−27 kg, is thus:
Applications and extensions
The components of an atom and of a nucleus have varying densities. The proton is not a fundamental particle, being composed of quark-gluon matter. Its size is approximately 10−15 meters and its density 1018 kg/m3. The descriptive term nuclear density is also applied to situations where similarly high densities occur, such as within neutron stars.
Using deep inelastic scattering, it has been estimated that the "size" of an electron, if it is not a point particle, must be less than 10−17 meters. This would correspond to a density of roughly 1021 kg/m3.
Probing deeper within particles, one finds quarks which appear to be very dense and very hard. There are possibilities for still higher densities when it comes to quark matter, gluon matter, or neutrino matter. In the immediate future, the highest experimentally measurable densities will likely be limited to leptons and quarks.
References
- "The Atomic Nucleus". Retrieved 2014-11-18. (derivation of equations and other mathematical descriptions)