Normal crossings
In algebraic geometry normal crossings is the property of intersecting geometric objects to do it in a transversal way.
Normal crossing divisors
In algebraic geometry, normal crossing divisors are a class of divisors which generalize the smooth divisors. Intuitively they cross only in a transversal way.
Let A be an algebraic variety, and 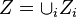 a reduced Cartier divisor, with
a reduced Cartier divisor, with 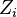 its irreducible components. Then Z is called a smooth normal crossing divisor if either
its irreducible components. Then Z is called a smooth normal crossing divisor if either
- (i) A is a curve, or
- (ii) all
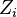 are smooth, and for each component
are smooth, and for each component  ,
, 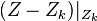 is a smooth normal crossing divisor.
is a smooth normal crossing divisor.
Equivalently, one says that a reduced divisor has normal crossings if each point étale locally looks like the intersection of coordinate hyperplanes.
Normal crossings singularity
In algebraic geometry a normal crossings singularity is a point in an algebraic variety that is locally isomorphic to a normal crossings divisor.
Simple normal crossings singularity
In algebraic geometry a simple normal crossings singularity is a point in an algebraic variety, the latter having smooth irreducible components, that is locally isomorphic to a normal crossings divisor.
Examples
- The normal crossing points in the algebraic variety called the Whitney umbrella are not simple normal crossings singularities.
- The origin in the algebraic variety defined by
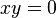 is a simple normal crossings singularity. The variety itself, seen as a subvariety of the two-dimensional affine plane is an example of a normal crossings divisor.
is a simple normal crossings singularity. The variety itself, seen as a subvariety of the two-dimensional affine plane is an example of a normal crossings divisor.
References
- Robert Lazarsfeld, Positivity in algebraic geometry, Springer-Verlag, Berlin, 1994.