Singular submodule

In the branches of abstract algebra known as ring theory and module theory, each right (resp. left) R module M has a singular submodule consisting of elements whose annihilators are essential right (resp. left) ideals in R. In set notation it is usually denoted as 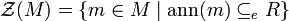$\mathcal{Z}(M)=\{m\in M \mid \mathrm{ann}(m)\subseteq_e R\}\,$ . For general rings, 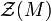$\mathcal{Z}(M)$ is a good generalization of the torsion submodule tors(M) which is most often defined for domains. 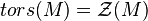In the case that R is a commutative domain, $tors(M)=\mathcal{Z}(M)$ .

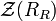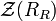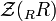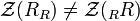If R is any ring, $\mathcal{Z}(R_R)$ is defined considering R as a right module, and in this case $\mathcal{Z}(R_R)$ is a twosided ideal of R called the right singular ideal of R. Similarly the left handed analogue $\mathcal{Z}(_R R)$ is defined. It is possible for $\mathcal{Z}(R_R)\neq\mathcal{Z}(_R R)$ .

Definitions

Here are several definitions used when studying singular submodule and singular ideals. In the following, M is an R module:

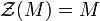M is called a singular module if $\mathcal{Z}(M)=M\,$ .
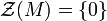M is called a nonsingular module if $\mathcal{Z}(M)=\{0\}\,$ .
R is called right nonsingular if 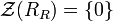$\mathcal{Z}(R_R)=\{0\}\,$ . A left nonsingular ring is defined similarly, using the left singular ideal, and it is entirely possible for a ring to be right-but-not-left nonsingular.

In rings with unity it is always the case that 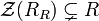$\mathcal{Z}(R_R)\subsetneq R\,$ , and so "right singular ring" is not usually defined the same way as singular modules are. Some authors have used "singular ring" to mean "has a nonzero singular ideal", however this usage is not consistent with the usage of the adjectives for modules.

Properties

Some general properties of the singular submodule include:

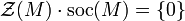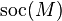$\mathcal{Z}(M)\cdot \mathrm{soc}(M)=\{0\}\,$ where $\mathrm{soc}(M)\,$ denotes the socle of M.
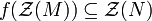If f is a homomorphism of R modules from M to N, then $f(\mathcal{Z}(M))\subseteq \mathcal{Z}(N)\,$ .
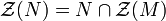If N is a submodule of M, then $\mathcal{Z}(N)=N\cap \mathcal{Z}(M)\,$ .
The properties "singular" and "nonsingular" are Morita invariant properties.
The singular ideals of a ring contain central nilpotent elements of the ring. Consequently the singular ideal of a commutative ring contains the nilradical of the ring.
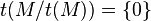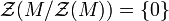A general property of the torsion submodule is that $t(M/t(M))=\{0\}\,$ , but this does not necessarily hold for the singular submodule. However if R is a right nonsingular ring, then $\mathcal{Z}(M/\mathcal{Z}(M))=\{0\}\,$ .
If N is an essential submodule of M (both right modules) then M/N is singular. If M is a free module, or if R is right nonsingular, then the converse is true.
A semisimple module is nonsingular if and only if it is a projective module.
If R is a right self-injective ring, then 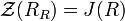$\mathcal{Z}(R_R)=J(R)\,$ , where J(R) is the Jacobson radical of R.

Examples

Right nonsingular rings are a very broad class, including reduced rings, right (semi)hereditary rings, von Neumann regular rings, domains, semisimple rings, Baer rings and right Rickart rings.

For commutative rings, being nonsingular is equivalent to being a reduced ring.

Important theorems

Johnson's Theorem (due to R. E. Johnson (Lam 1999, p. 376)) contains several important equivalences. For any ring R, the following are equivalent:

R is right nonsingular.
The injective hull E(R_R) is a nonsingular right R module.
The endomorphism ring 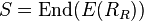$S=\mathrm{End}(E(R_R))\,$ is a semiprimitive ring (that is, $J(S)=\{0\}\,$ ).
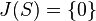The maximal right ring of quotients 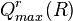$Q_{max}^r(R)$ is von Neumann regular.

Right nonsingularity has a strong interaction with right self injective rings as well.

Theorem: If R is a right self injective ring, then the following conditions on R are equivalent: right nonsingular, von Neumann regular, right semihereditary, right Rickart, Baer, semiprimitive. (Lam 1999, p. 262)

The paper (Zelmanowitz 1983) used nonsingular modules to characterize the class of rings whose maximal right ring of quotients have a certain structure.

Theorem: If R is a ring, then 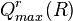$Q_{max}^r(R)$ is a right full linear ring if and only if R has a nonsingular, faithful, uniform module. Moreover, 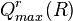$Q_{max}^r(R)$ is a finite direct product of full linear rings if and only if R has a nonsingular, faithful module with finite uniform dimension.

Textbooks

Goodearl, K. R. (1976), Ring theory: Nonsingular rings and modules, Pure and Applied Mathematics, No. 33, New York: Marcel Dekker Inc., pp. viii+206, MR 0429962
Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98428-5, MR 1653294

Primary sources

Zelmanowitz, J. M. (1983), "The structure of rings with faithful nonsingular modules", Trans. Amer. Math. Soc. 278 (1): 347–359, doi:10.2307/1999320, ISSN 0002-9947, MR 697079 84d:16030)

This article is issued from Wikipedia - version of the Friday, June 05, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.