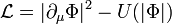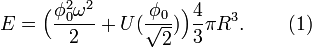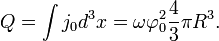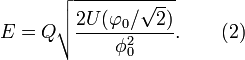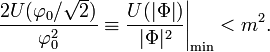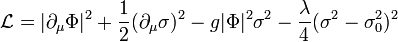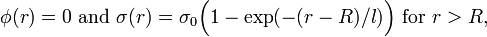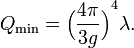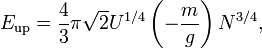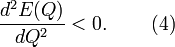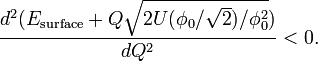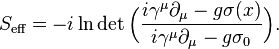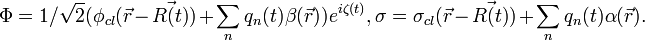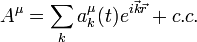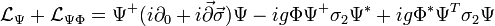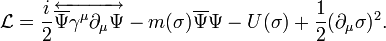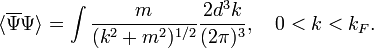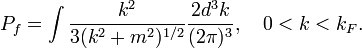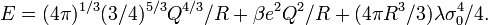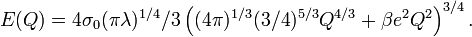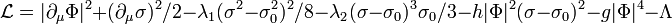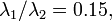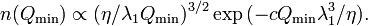Non-topological soliton
In quantum field theory, a non-topological soliton (NTS) is a field configuration possessing, contrary to a topological one, a conserved Noether charge and stable against transformation into usual particles of this field for the following reason. For fixed charge Q, the mass sum of Q free particles exceeds the energy (mass) of the NTS so that the latter is energetically favorable to exist.
The interior region of an NTS is occupied by vacuum different from surrounding one. Thus a surface of the NTS represents a domain wall, which also appears as a topological defect in field theories with broken discrete symmetry.[1] If infinite, the domain walls cause contradiction with cosmology. But the surface of an NTS is a closed finite wall so, if it exists in the Universe, it does not cause those contradictions. Another point is that if the topological domain wall is closed, it shrinks because of wall tension. As for the NTS surface,it does not shrink since the decreasing of the NTS volume would increase its energy.
Introduction
Quantum field theory has been developed to describe the elementary particles. However in the mid seventies it was found out that this theory predicts one more class of stable compact objects: non-topological solitons. The NTS represents an unusual coherent state of matter, called also bulk matter. Models were suggested for the NTS to exist in forms of stars, quasars, the dark matter and nuclear matter.
An NTS configuration is the lowest energy solution of classical equations of motion possessing a spherical symmetry. Such a solution has been found for a rich variety of field Lagrangians. One can associate the conserved charge with global, local, Abelian and non-Abelian symmetry. It appears to be possible the NTS configuration with bosons as well as with fermions to exist. In different models either one and the same field carries the charge and binds the NTS, or there are two different fields: charge carrier and binding field.

The spatial size of the NTS configuration may be elementary small or astronomically large: depending on a model, i.e. the model fields and constants. The NTS size could increase with its energy until the gravitation complicates its behavior and finally causes the collapse. Although in some models the NTS charge is bounded by the stability (or metastability) condition.
Simple examples
One field
For a complex scalar field with the U(1) invariant Lagrange density[2]
the NTS is a ball with radius R filled with the field 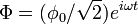 . Here
. Here 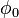 is a constant inside the ball except for a thin surface coat where it sharply drops to the global U(1) symmetrical minimum of
is a constant inside the ball except for a thin surface coat where it sharply drops to the global U(1) symmetrical minimum of 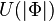 . The value
. The value 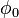 is adjusted so that it minimises the energy of the configuration
is adjusted so that it minimises the energy of the configuration
Since the U(1) symmetry gives the conserved current 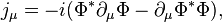
the ball possesses the conserved charge
The minimization of the energy (1) with R gives
The charge conservation allows the decay of the ball into Q particles exactly. This decay is energetically unprofitable if the sum mass Qm exceed the energy (2). Therefore for the NTS existence it is necessary to have
The thin wall approximation, which was used above, allows to omit the gradient term 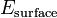 in the expression for energy (1), since
in the expression for energy (1), since 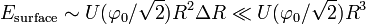 . This approximation is valid for
. This approximation is valid for 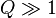 and is justified by the exact solution of the motion equation.
and is justified by the exact solution of the motion equation.
Two fields
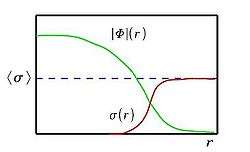
The NTS configuration for a couple of interacting scalar fields[3] is sketched here. The Lagrange density
is invariant under U(1) transformation of the complex scalar field 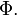 Let this field depends on time and coordinate simply as
Let this field depends on time and coordinate simply as 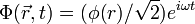 . It carries the conserved charge
. It carries the conserved charge 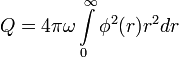 . In order to check that the energy of the configuration is smaller than Qm, one should either to calculate this energy numerically or to use the variational method. For trial functions
. In order to check that the energy of the configuration is smaller than Qm, one should either to calculate this energy numerically or to use the variational method. For trial functions
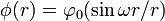 and
and 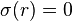 for r < R,
for r < R,
the energy in the large Q limit is approximately equal to
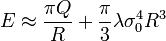 .
.
The minimization with R gives the upper estimation 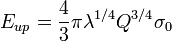
for the energy of the exact solution of motion equations
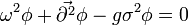 and
and 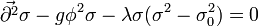 .
.
It is indeed smaller than 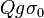 for Q exceeding the crucial charge
for Q exceeding the crucial charge
Fermion plus scalar
If instead of boson, fermions carry the conserved charge, an NTS also exists. At this time one could take
N is the number of fermion species in the theory. Q can't exceed N due to the Pauli exclusive principle if the fermions are in the coherent state. This time the NTS energy E is bound by
See Friedberg/Lee.[4]
Stability
Classical stability
The condition 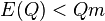 only allows to assert the NTS stability against a decay into free particles. The equation of motion gives
only allows to assert the NTS stability against a decay into free particles. The equation of motion gives 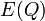 only on a classical level. At least two things should be take into account: (i) the decay into smaller pieces (fission) and (ii) the quantum correction for
only on a classical level. At least two things should be take into account: (i) the decay into smaller pieces (fission) and (ii) the quantum correction for 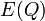 .
.

The condition of stability against the fission looks as follows:
It signifies that 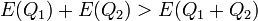 . This condition is satisfied for the NTS in examples 2.2 and 2.3. The NTS in example 2.1, called also Q-ball, is stable against the fission as well, even though the energy (2) does not satisfy (4): one has to recollect the omitted gradient surface energy and to add it to the Q-ball energy (1). Perturbatively,
. This condition is satisfied for the NTS in examples 2.2 and 2.3. The NTS in example 2.1, called also Q-ball, is stable against the fission as well, even though the energy (2) does not satisfy (4): one has to recollect the omitted gradient surface energy and to add it to the Q-ball energy (1). Perturbatively, 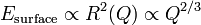 . Thus
. Thus
Another job 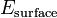 does, is to set
does, is to set 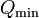 for the thin-wall description of Q-ball: for small Q the surface becomes thicker,
for the thin-wall description of Q-ball: for small Q the surface becomes thicker, 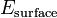 grows and kills the energy gain
grows and kills the energy gain 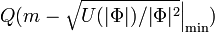 . However the formalism for the thick-wall approximation has been developed by Kusenko[5] who says that for small Q, NTS also exists.
. However the formalism for the thick-wall approximation has been developed by Kusenko[5] who says that for small Q, NTS also exists.
Quantum correction
As for quantum correction, it also diminishes the binding energy per charge 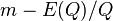 for small NTS, making them unstable. The small NTS are especially important for the fermion case, since it is naturally to expect rather small number of fermions species N in (3), and consequently, Q. For Q=2 the quantum correction decreases the binding energy by 23%.[6]
For Q=1 a calculation based on the path integral method has been carried out by Baacke.[7]
The quantum energy has been derived as a time derivative of the one-loop fermion effective action
for small NTS, making them unstable. The small NTS are especially important for the fermion case, since it is naturally to expect rather small number of fermions species N in (3), and consequently, Q. For Q=2 the quantum correction decreases the binding energy by 23%.[6]
For Q=1 a calculation based on the path integral method has been carried out by Baacke.[7]
The quantum energy has been derived as a time derivative of the one-loop fermion effective action
This calculation gives the loop energy of the order of binding energy. In order to find the quantum correction following the canonical method of quantization, one has to solve the Schrödinger equation for the Hamiltonian built with quantum expansion of field functions. For the boson field NTS[3] it reads
Here 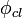 and
and 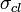 are the solutions of the classical equation of motion,
are the solutions of the classical equation of motion, 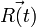 represents motion of the mass center,
represents motion of the mass center, 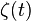 is the over-all phase,
is the over-all phase, 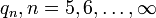 are the vibration coordinates, by analogy with the oscillator decomposition of photon field
are the vibration coordinates, by analogy with the oscillator decomposition of photon field
For this calculation the smallness of four-interaction constant is essential, since the Hamiltonian is taken in the lowest order of that constant. The quantum decreasing of the binding energy increases the minimal charge 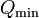 making the NTS metastable between old and new values of this charge.
making the NTS metastable between old and new values of this charge.

NTSs in some models become unstable as Q exceeds some stable charge 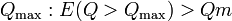 . For example, NTS with fermions carrying a gauge charge[8] has
. For example, NTS with fermions carrying a gauge charge[8] has 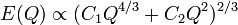 exceeding Qm for Q large enough as well as for small one. Besides, the gauged NTS probably is unstable against a classical decay without conservation of its charge due to complicated vacuum structure of the theory.[9]
Generally, the NTS charge is limited by the gravitational collapse:
exceeding Qm for Q large enough as well as for small one. Besides, the gauged NTS probably is unstable against a classical decay without conservation of its charge due to complicated vacuum structure of the theory.[9]
Generally, the NTS charge is limited by the gravitational collapse:
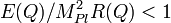 .
.
Particle emission
If one adds to the Q-ball Lagrange density an interaction with massless fermion 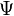
which is also U(1) invariant assuming the global charge for boson twice as for fermion, Q-ball once created begins to emit its charge with 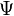 -pairs, predominantly from its surface. The evaporation rate per unit area[10]
-pairs, predominantly from its surface. The evaporation rate per unit area[10] 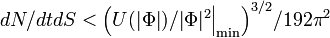 .
.
The ball of trapped right-handed Majorana neutrinos in 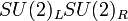 symmetric electroweak theory loses its charge (the number of trapped particles) through the neutrino-antineutrino annihilation by emitting photons from the whole volume.[11][12]
symmetric electroweak theory loses its charge (the number of trapped particles) through the neutrino-antineutrino annihilation by emitting photons from the whole volume.[11][12]
The third example for a NTS metastable due to particle emission is the gauged non-Abelian NTS. The massive (outside the NTS) member of fermionic multiplet decays into a massless one and a gauged boson also massless in the NTS. Then the massless fermion carries away the charge since it does not interact at all with the Higgs fied.
Three last examples represent a class for NTS metastable due to emission of particles which do not participate in the NTS construction. One more similar example: because of the Dirac mass term 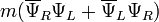 , right-handed neutrinos convert to left-handed ones. That happens at the surface of neutrino ball mentioned above. Left-handed neutrinos are very heavy inside the ball and they are massless outside it. So they go away carrying the energy and diminishing the number of particles inside. This "leakage" appears to be much slower than the annihilation onto photons.[13]
, right-handed neutrinos convert to left-handed ones. That happens at the surface of neutrino ball mentioned above. Left-handed neutrinos are very heavy inside the ball and they are massless outside it. So they go away carrying the energy and diminishing the number of particles inside. This "leakage" appears to be much slower than the annihilation onto photons.[13]
Soliton-stars
Q-star
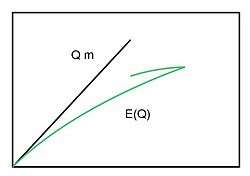
As the charge Q grows and E(Q) the order of 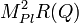 , the gravitation becomes important for NTS. A proper name for such an object is a star. A boson-field Q-star looks like a big Q-ball. The way gravity changes E(Q) dependence[14] is sketched here. It is the gravity what makes
, the gravitation becomes important for NTS. A proper name for such an object is a star. A boson-field Q-star looks like a big Q-ball. The way gravity changes E(Q) dependence[14] is sketched here. It is the gravity what makes 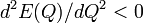 for Q-star — stabilize it against the fission.
for Q-star — stabilize it against the fission.
Q-star with fermions has been described by Bahcall/Selipsky.[15] Similar the NTS of Friedberg & Lee, the fermion field carrying a global conserved charge, interacts with a real scalar field.
The 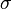 inside Q-star moves from a global maximum of the potential changing the mass of fermions and making them bound.
inside Q-star moves from a global maximum of the potential changing the mass of fermions and making them bound.
But this time Q is not the number of different fermion species but it is the large number of one and the same kind particles in the Fermi gas state. Then for the fermion field description one has to use 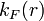 instead of
instead of 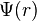 and the condition of pressure equilibrium instead of the Dirac equation for
and the condition of pressure equilibrium instead of the Dirac equation for 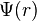 . Another unknown function is the scalar field
. Another unknown function is the scalar field 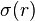 profile which obeys the following motion equation :
profile which obeys the following motion equation : 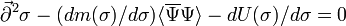 . Here
. Here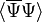 is the scalar density of fermions, averaged on statistical ensemble:
is the scalar density of fermions, averaged on statistical ensemble:
Fermi energy of the fermion gas 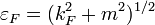 .
.
Neglecting the derivatives of 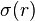 for large Q, that equation together with the pressure equilibrium equation
for large Q, that equation together with the pressure equilibrium equation 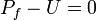 , constitute a simple system which gives
, constitute a simple system which gives 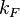 and
and 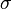 inside the NTS. They are constant since we have neglected the derivatives. The fermion pressure
inside the NTS. They are constant since we have neglected the derivatives. The fermion pressure
For example if 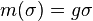 and
and 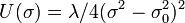 , then
, then 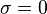 and
and 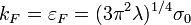 . That means fermions appear to be massless in the NTS. Then the full fermion energy
. That means fermions appear to be massless in the NTS. Then the full fermion energy 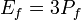 . For an NTS with the volume
. For an NTS with the volume  and the charge
and the charge 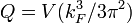 , its energy is proportional to the charge:
, its energy is proportional to the charge: 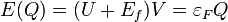 .
.
The described above fermion Q-star has been considered as a model for neutron star[16][17] in the effective hadron field theory.
Soliton star
If the scalar field potential 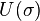 has two degenerate or almost degenerate minima, one of them have to be the real (true) minimum in which we happen to leave. Inside NTS
has two degenerate or almost degenerate minima, one of them have to be the real (true) minimum in which we happen to leave. Inside NTS 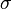 occupies another one. In such a model non-zero vacuum energy appears only at the NTS surface, not in its volume. This allows for the NTS to be very big without falling in gravitational collapse.
occupies another one. In such a model non-zero vacuum energy appears only at the NTS surface, not in its volume. This allows for the NTS to be very big without falling in gravitational collapse.
That is the case in the left-right symmetric electroweak theory. For a scale of symmetry breaking about 1 TeV, 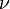 -ball of trapped right-haded massless neutrino might have the mass (energy) about 108 solar masses and was considered as a possible model for quasar.[18]
-ball of trapped right-haded massless neutrino might have the mass (energy) about 108 solar masses and was considered as a possible model for quasar.[18]
For the degenerate potential 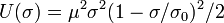 both boson[19] and fermion[20] soliton stars were investigated.
both boson[19] and fermion[20] soliton stars were investigated.
A complex scalar field could alone form the state of gravitational equilibrium possessing the astronomically large conserved number of particles.[21][22] Such objects are called minisoliton stars because of their microscopic size.
Non-topological soliton with standard fields
Could a system of the Higgs field and some fermion field of the Standard model be in the state of Friedberg & Lee NTS ? That is more possible for a heavy fermion field: for a such one the energy gain would be the most because it does lose its large mass in the NTS interior, were the Yukawa term 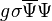 vanishes due to
vanishes due to 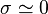 . The more so if the vacuum energy in the NTS interior
. The more so if the vacuum energy in the NTS interior 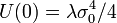 is large, that would mean the large Higgs mass
is large, that would mean the large Higgs mass 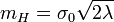 . The large fermion mass implies strong Yukawa coupling
. The large fermion mass implies strong Yukawa coupling  .
.
Calculation shows[23] that the NTS solution is energetically favored over a plane wave (free particle) only if 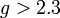 for even very small
for even very small 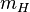 . For
. For
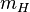 =350 GeV (this is the point were
=350 GeV (this is the point were 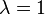 for experimentally known
for experimentally known 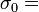 250 GeV) the coupling
250 GeV) the coupling  must be more than five.
must be more than five.
The next question is whether or not multi-fermion NTS like a fermion Q-star is stable in the Standard model. If we restrict ourself by one fermion species, then the NTS has god the gauge charge. One can estimate the energy of gauged NTS as follows:
Here  and
and 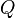 are its radius and charge, the first term is the kinetic energy of the fermi-gas, the second is the Coulomb energy,
are its radius and charge, the first term is the kinetic energy of the fermi-gas, the second is the Coulomb energy, 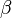 takes into account the charge distribution inside the NTS and the latest one gives the volume vacuum energy. Minimization with
takes into account the charge distribution inside the NTS and the latest one gives the volume vacuum energy. Minimization with  gives the NTS energy as a function of its charge:
gives the NTS energy as a function of its charge:
An NTS is stable if 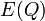 is smaller than the sum of masses for
is smaller than the sum of masses for 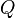 particles at infinite distance each from other. That is case for some
particles at infinite distance each from other. That is case for some 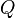 , but such a
, but such a 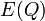 dependence allows the fission for any
dependence allows the fission for any 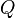 .
.
Why could not quarks be bound in a hadron like in NTS. Friedberg and Lee investigated such a possibility.[6] They assumed quarks getting huge masses from their interaction with a scalar field 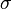 . Thus free quarks are heavy and escape from detection. The NTS built with quarks and
. Thus free quarks are heavy and escape from detection. The NTS built with quarks and 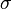 fields demonstrate static properties of hadrons with 15% accuracy. That model demands SU(3) symmetry additional to the color one in order to preserve the later unbroken so that QCD gluons get large masses by SU(3) symmetry breaking outside hadrons and also avoid detection.
fields demonstrate static properties of hadrons with 15% accuracy. That model demands SU(3) symmetry additional to the color one in order to preserve the later unbroken so that QCD gluons get large masses by SU(3) symmetry breaking outside hadrons and also avoid detection.
Nuclei have been considered as NTS's in the effective theory of strong interaction which is easier to deal with than QCD.[17][24]
Solitonogenesis
Trapped particles
The way NTS's could be born by depends on whether or not the Universe carries a net charge. If it does not then NTS could be formed from random fluctuations of the charge. Those fluctuations grow up, disturb the vacuum and create NTS configurations.
If the net charge is present, i.e. charge asymmetry exists with a parameter 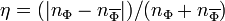 , NTS could be simply born as the space became divided onto finite regions of true and false vacuum during the phase transition in the early Universe. Those occupied by the NTS (false) vacuum are almost ready NTSs. The scenario of the region formation depends on the phase transition order.
, NTS could be simply born as the space became divided onto finite regions of true and false vacuum during the phase transition in the early Universe. Those occupied by the NTS (false) vacuum are almost ready NTSs. The scenario of the region formation depends on the phase transition order.

If the first order phase transition occurs, then nucleating bubbles of true vacuum grow and percolate, shrinking regions filled with the false vacuum. The later are preferable for charged particles to live in due to their smaller masses, so those regions become NTSs.

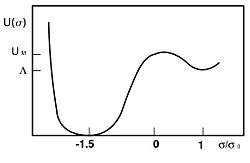
In case of the second order phase transition as temperature drops below the crucial value  the space consist of interconnecting regions of both false and true vacua with characteristic size
the space consist of interconnecting regions of both false and true vacua with characteristic size 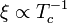 . This interconnection "freezes out" as its rate becomes smaller than the expansion rate of the Universe at Ginzburg temperature
. This interconnection "freezes out" as its rate becomes smaller than the expansion rate of the Universe at Ginzburg temperature 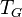 , then the regions of two vacua percolate.
, then the regions of two vacua percolate.
But if the false vacuum energy is large enough, 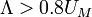 on the plot, the false vacuum forms finite clusters (NTS's) surrounded by the percolated true vacuum.[25]
The trapped charge stabilizes clusters against collapse.
on the plot, the false vacuum forms finite clusters (NTS's) surrounded by the percolated true vacuum.[25]
The trapped charge stabilizes clusters against collapse.
In the second scenario of the NTS formation the number of born 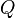 -charged NTS's per unit volume is simply the number density of clusters holding
-charged NTS's per unit volume is simply the number density of clusters holding 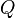 particles. Their number density is given[26]
by
particles. Their number density is given[26]
by 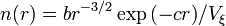 , here b and c are constants of the order of unit,
, here b and c are constants of the order of unit, 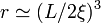 is the number of correlation volumes
is the number of correlation volumes 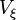 in a cluster of size
in a cluster of size  . The number of particle in a cluster is
. The number of particle in a cluster is
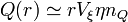 , here
, here 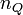 is the charge density in the universe at Ginzburg temperature. Thus big clusters are born very rarely and if the minimum stable charge
is the charge density in the universe at Ginzburg temperature. Thus big clusters are born very rarely and if the minimum stable charge 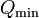 is present, then overwhelming majority of born NTS carries
is present, then overwhelming majority of born NTS carries 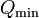 .
.
For the following Lagrange density with biased discrete symmetry[27]
with
-
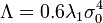 and
and 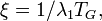
it appears to be 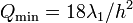 and
and
Field condensate
The net charge could be also placed in the complex scalar field condensate 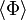 instead of free particles. This condensate could consist of spatially homogeneous
instead of free particles. This condensate could consist of spatially homogeneous 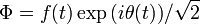 and
and
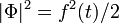 provides its potential to be at minimum as the universe cools down and the temperature correction changes the form of the potential. Such a model was treated to explain the baryon asymmetry.[28]
provides its potential to be at minimum as the universe cools down and the temperature correction changes the form of the potential. Such a model was treated to explain the baryon asymmetry.[28]
If the field potential allows Q-ball to exist, then they could be born from this condensate as the charge volume density 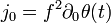 drops in course of the universe expansion and becomes equal to Q-balls charge density.[29]
As follows from the equation of motion for
drops in course of the universe expansion and becomes equal to Q-balls charge density.[29]
As follows from the equation of motion for 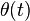 , this density
, this density 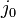 changes with the expansion as the minus third power of scale factor
changes with the expansion as the minus third power of scale factor 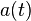 for the expanding space-time with the differential length element
for the expanding space-time with the differential length element 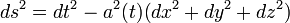 .
.
Breaking the condensate onto Q-balls appears to be favorable over further dilution of the homogeneous charge density by expansion. The total charge in a comoving volume 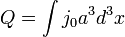 stays fixed of course.
stays fixed of course.
The condensation of  could occur at high temperature of the universe, due to the negative temperature correction to its mass:
could occur at high temperature of the universe, due to the negative temperature correction to its mass: 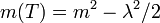 which provides with minimum its potential
which provides with minimum its potential 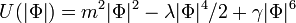 . Here the last term is induced by the interaction
. Here the last term is induced by the interaction 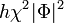 with additional field
with additional field  that has to be introduced in order to satisfy the Q-ball existence condition
that has to be introduced in order to satisfy the Q-ball existence condition 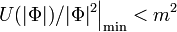 . At the temperature relevant to relevant Q-balls formation
. At the temperature relevant to relevant Q-balls formation  appears only through virtual process (loops) because it is heavy. An alternative way to satisfy the Q=ball existence condition is to appeal to the non-Abelian symmetry.[30]
appears only through virtual process (loops) because it is heavy. An alternative way to satisfy the Q=ball existence condition is to appeal to the non-Abelian symmetry.[30]
Further evolution
Once formed, the NTSs undergo complicated evolution, losing and acquiring the charge by interaction with each other and surrounding particles. Depending on theory parameters, they could either disappear at all or get statistical equilibrium and "freeze out" at some temperature of the universe, or be born "frozen out" if their interaction is slower than expansion rate at 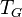 . In the first and the second cases, their up-to-date abundance (if any) has nothing to do with that at the moment of formation.[31][32]
. In the first and the second cases, their up-to-date abundance (if any) has nothing to do with that at the moment of formation.[31][32]
Since an NTS is a composite object, it has to demonstrate properties different from those of a single particle, e.g. evaporation emission, excitation levels, scattering form-factor. Cosmic observations of such phenomena could provide the unique information about the physics beyond the ability of accelerators.
References
- ↑ A. Vilenkin, Phys. Rep. 121(1985) 263.
- ↑ S. Coleman, Nucl. Phys. B 262(1985)263.
- 1 2 R. Friedberg, T. D. Lee, A. Sirlin, Phys, Rev. D 13 (1976) 2739.
- ↑ R. Friedberg, T. D. Lee, Phys. Rev. D 15(1977)1694.
- ↑ A. Kusenko, CERN-Th/97-69, hep-th/9704073
- 1 2 R. Friedberg, T. D. Lee, Phys. Rev. D 16 (1977) 1096.
- ↑ J. Baacke, DO-TH/90-5.
- ↑ K. Lee, J. A. Stein-Shabes, R. Watkins, L. M. Widrow, Phys. Rev. D 39 (1989) 1665.
- ↑ G. G. Petriashvilly, Yad. Phys. 50 (1989) 573.
- ↑ A. Cohen, S. Coleman, H. Georgi, A. Manohar, Nucl. Phys. B 272 (1986) 301.
- ↑ B. Holdom, Phys. Rev. D 36 (1987) 1000.
- ↑ A. D. Dolgov, O. Yu. Markin, Sov. Phys. JETP 71 (1990) 207.
- ↑ A. E. Everett, Phys. Rev. D 10 (1974) 3126.
- ↑ B. W. Lynn, Nucl. Phys. B 321 (1989) 465.
- ↑ S. Bahcall, B. W. Lynn, S. B. Selipsky, Nucl. Phus. B 325 (1989) 606.
- ↑ S. Bahcall, B. W. Lynn, S. B. Selipsky, Preprint SU-ITP-866 (1989).
- 1 2 S. Bahcall, B. W. Lynn, S. B. Selipsky, Nucl. Phus. B 331 (1990) 67.
- ↑ A. D. Dolgov, O. Yu. Markin, Progr. Theor. Phys. 85 (1991) 1091.
- ↑ R. Friedberg, T. D. Lee, Y. Pang, Phys. Rev. D 35 (1987) 3640.
- ↑ T. D. Lee, Y. Pang, Phys. Rev. D 35 (1987) 3678.
- ↑ R. Friedberg, T. D. Lee, Y. Pang, Phys. Rev. D 35 (1987) 3658.
- ↑ J. J. Van der Bij, M. Gleiser, Preprint FERMILAB-Pub-87/41-A.
- ↑ S. Dimopoulos, B. W. Lynn, S. Selipsky, N. Tetradis, Preprint CERN-TH.5761/90.
- ↑ D. A. Hochron, Preprint CERN-TH-5991/91.
- ↑ G. Gelmini, M. Gleiser, E. Kolb, Phys. Rev. D 39 (1989) 1558.
- ↑ D. Stauffer, Phys. Rep. 54(1979)1.
- ↑ J. A. Frieman, G. B. Gelmini, N. Gleiser, E. W. Kolb, Phys. Rev. Lett. 60(1988)2101.
- ↑ S. Dodelson, L. M. Widrow, Phys. Rev. Lett. 41(1990)340.
- ↑ K. M. Benson, L. M. Widrow, Preprint HUTP-90/A054.
- ↑ A. M. Safian, S. Coleman, M. Axenides, Nucl. Phys. B 297(1988)498.
- ↑ K. Griest, E. W. Kolb, Phys. Rev. D 40(1989)3529.
- ↑ J. A. Frieman, A. V. Olinto, M. Gleiser, C. Alcock, Phys. Rev. D 40(1989)3241.