Non-exact solutions in general relativity

Non-exact solutions in general relativity are solutions of Albert Einstein's field equations of general relativity which hold only approximately. These solutions are typically found by treating the gravitational field, $g$ , as a background space-time, $\gamma$ , (which is usually an exact solution) plus some small perturbation, $h$ . Then one is able to solve the Einstein field equations as a series in $h$ , dropping higher order terms for simplicity.

A common example of this method results in the linearised Einstein field equations. In this case we expand the full space-time metric about the flat Minkowski metric, 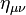$\eta_{\mu\nu}$ :

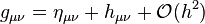g_{\mu\nu} = \eta_{\mu\nu} + h_{\mu\nu} +\mathcal{O}(h^2)

and dropping all terms which are of second or higher order in $h$ .^[1]

References

↑ Sean M. Carroll (2004). Spacetime and Geometry: An Introduction to General Relativity. Addison-Wesley Longman, Incorporated. pp. 274–279. ISBN 978-0-8053-8732-2.

This article is issued from Wikipedia - version of the Wednesday, January 08, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Non-exact solutions in general relativity

See also

References