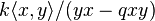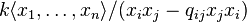Noncommutative projective geometry

In mathematics, noncommutative projective geometry is a noncommutative analog of projective geometry in the setting of noncommutative algebraic geometry.

Examples

• The quantum plane, the most basic example, is the quotient ring of the free ring:

• More generally, the quantum polynomial ring is the quotient ring:

Proj construction

By definition, the Proj of a graded ring R is the quotient category of the category of finitely generated graded modules over R by the subcategory of torsion modules. If R is a commutative Noetherian graded ring generated by degree-one elements, then the Proj of R in this sense is equivalent to the category of coherent sheaves on the usual Proj of R. Hence, the construction can be thought of as a generalization of the Proj construction for a commutative graded ring.

See also

• Elliptic algebra
• Calabi–Yau algebra

References

• Ajitabh, Kaushal (1994), Modules over regular algebras and quantum planes (PDF) (Ph.D. thesis) 
• Artin M.: Geometry of quantum planes, Contemporary Mathematicsv. 124 (1992).
• Rogalski, D (2014). "An introduction to Noncommutative Projective Geometry". arXiv:1403.3065.