Nilpotent space

In topology, a branch of mathematics, a nilpotent space is a based topological space X such that the fundamental group 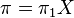$\pi = \pi_1 X$ is a nilpotent group and 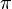$\pi$ acts nilpotently on higher homotopy groups 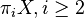$\pi_i X, i \ge 2$ .^[1] A simply connected space and a simple space are (trivial) examples of nilpotent spaces.

References

↑ Bousfield, A. K.; Kan, D. M. (1987), Homotopy Limits, Completions and Localizations, Lecture Notes in Mathematics 304, Springer, p. 59, ISBN 9783540061052 .

This article is issued from Wikipedia - version of the Monday, March 10, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.