Nice name
In set theory, a nice name is used in forcing to impose an upper bound on the number of subsets in the generic model. It is used in the context of forcing to prove independence results in set theory such as Easton's theorem.
Formal definition
Let 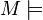 ZFC be transitive,
ZFC be transitive, 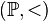 a forcing notion in
a forcing notion in 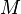 , and suppose
, and suppose 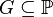 is generic over
is generic over 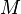 . Then for any
. Then for any 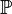 -name in
-name in 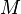 ,
, 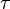 ,
,
 is a nice name for a subset of
is a nice name for a subset of 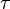 if
if  is a
is a 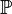 -name satisfying the following properties:
-name satisfying the following properties:
(1) 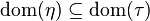
(2) For all 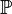 -names
-names 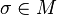 ,
, 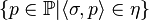 forms an antichain.
forms an antichain.
(3) (Natural addition): If 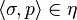 , then there exists
, then there exists 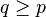 in
in 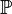 such that
such that 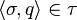 .
.
References
- Kenneth Kunen (1980) Set theory: an introduction to independence proofs, Volume 102 of Studies in logic and the foundations of mathematics (Elsevier) ISBN 0-444-85401-0, p.208
This article is issued from Wikipedia - version of the Sunday, November 22, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.