Atkin–Lehner theory

In mathematics, Atkin–Lehner theory is part of the theory of modular forms, in which the concept of newform is defined in such a way that the theory of Hecke operators can be extended to higher level. A newform is a cusp form 'new' at a given level N, where the levels are the nested subgroups

Γ₀(N)

of the modular group, with N ordered by divisibility. That is, if M divides N, Γ₀(N) is a subgroup of Γ₀(M). The oldforms for Γ₀(N) are those modular forms f(τ) of level N of the form g(d τ) for modular forms g of level M with M a proper divisor of N, where d divides N/M. The newforms are defined as a vector subspace of the modular forms of level N, complementary to the space spanned by the oldforms, i.e. the orthogonal space with respect to the Petersson inner product.

The Hecke operators, which act on the space of all cusp forms, preserve the subspace of newforms and are self-adjoint and commuting operators (with respect to the Petersson inner product) when restricted to this subspace. Therefore, the algebra of operators on newforms they generate is a finite-dimensional C*-algebra that is commutative; and by the spectral theory of such operators, there exists a basis for the space of newforms consisting of eigenforms for the full Hecke algebra.

Involutions

In the congruence subgroup Γ(N), the matrix elements are taken from the ring ℤ_N of integers modulo N. Its subgroup

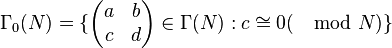\Gamma_0(N) = \{ \begin{pmatrix}a & b \\c & d \end{pmatrix} \isin \Gamma (N) : c \cong 0 (\mod N) \}

contains translations on the projective line over Z_N.

But Γ₀(N) is not a normal subgroup of Γ(N), it requires extension by elements of the form

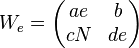W_e = \begin{pmatrix}ae & b \\ cN & de \end{pmatrix}

where det W_e = e and e is a maximal divisor of N. Not only does e divide N, but also e and N/e are relatively prime. Notation for maximal divisor e is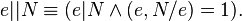

e || N \equiv (e|N \and (e, N/e) = 1 ).

Then 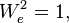$W_e^2 = 1 ,$ so it is an involution, and is called an Atkin-Lehmer involution. If e and f are both maximal divisors of N, then W_e and W_f commute and their product is W_g where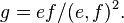 $g = e f/(e,f)^2 .$

If there are s distinct primes dividing N, then the normalizer Γ₀(N) + is a extension of Γ₀(N) such that the quotient group is an abelian group of order 2^s.^[1]

References

↑ Koichiro Harada (2010) Moonshine of Finite Groups, page 13

Atkin, A. O. L.; Lehner, J. (1970), "Hecke operators on Γ₀ (m)", Mathematische Annalen 185: 134–160, doi:10.1007/BF01359701, ISSN 0025-5831, MR 0268123

This article is issued from Wikipedia - version of the Saturday, February 13, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.