Neutron reflectometry
| Science with Neutrons |
|---|
 |
| Foundations |
| Neutron scattering |
| Other applications |
|
| Infrastructure |
|
| Neutron facilities |
Neutron reflectometry is a neutron diffraction technique for measuring the structure of thin films, similar to the often complementary techniques of X-ray reflectivity and ellipsometry. The technique provides valuable information over a wide variety of scientific and technological applications including chemical aggregation, polymer and surfactant adsorption, structure of thin film magnetic systems, biological membranes, etc.
Technical details
The technique involves shining a highly collimated beam of neutrons onto an extremely flat surface and measuring the intensity of reflected radiation as a function of angle or neutron wavelength. The exact shape of the reflectivity profile provides detailed information about the structure of the surface, including the thickness, density, and roughness of any thin films layered on the substrate.
Neutron reflectometry is a specular reflection technique, where the angle of the incident beam is equal to the angle of the reflected beam. The reflection is usually described in terms of a momentum transfer vector, denoted 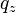 , which describes the change in momentum of a neutron after reflecting from the material. Conventionally the
, which describes the change in momentum of a neutron after reflecting from the material. Conventionally the 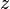 direction is defined to be the direction normal to the surface, and for specular reflection, the scattering vector has only a
direction is defined to be the direction normal to the surface, and for specular reflection, the scattering vector has only a 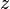 -component. A typical neutron reflectometry plot displays the reflected intensity (relative to the incident beam) as a function of the scattering vector:
-component. A typical neutron reflectometry plot displays the reflected intensity (relative to the incident beam) as a function of the scattering vector:
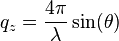
where  is the neutron wavelength, and
is the neutron wavelength, and  is the angle of incidence. The Abeles matrix formalism or the Parratt recursion can be used to calculate the specular signal arising from the interface.
is the angle of incidence. The Abeles matrix formalism or the Parratt recursion can be used to calculate the specular signal arising from the interface.
The wavelength of the neutrons used for reflectivity are typically on the order of 0.2 to 1 nm (2 to 10 Å). This technique requires a neutron source, which may be either a research reactor or a spallation source (based on a particle accelerator). Like all neutron scattering techniques, neutron reflectometry is sensitive to contrast arising from different nuclei (as compared to electron density, which is measured in x-ray scattering). This allows the technique to differentiate between various isotopes of elements. Neutron reflectometry measures the neutron scattering length density (SLD) and can be used to accurately calculate material density if the atomic composition is known.
Neutron scattering lengths
A neutron may pass by a nucleus with a probability determined by the nuclear interaction distance, or be absorbed, or undergo scattering that may be either coherent or incoherent.[1] The scattering length of neutrons varies by element and isotope in a way that appears random, whereas the scattering of X-rays generally increases with the atomic number.[1][2]
The scattering length may be either positive or negative. The scattering cross-section is equal to the square of the scattering length multiplied by 4π,[3] i.e. the area of a circle with radius twice the scattering length. In some cases, as with titanium and niobium, it is possible to mix isotopes of an element whose lengths are of opposite signs to give a net scattering length of zero, in which case coherent scattering will not occur at all. However, neutrons will still undergo strong incoherent scattering in these materials.[1]
There is a large difference in scattering length between protium (-0.374) and deuterium (0.667). This means that protium, the most common isotope of hydrogen, is poorly imaged due to its smaller absolute magnitude and because its scattering density tends to cancel that of adjacent carbon, nitrogen, or oxygen, which have positive scattering lengths. Because of these factors, as well as the much larger incoherent scattering cross section of protium, ordinary proteins cannot be imaged as well as those that are fully deuterated. Specific exchangeable hydrogens in a non-deuterated protein may be imaged if it is exposed to heavy water.[4]
| element | protons | isotope | X-ray scattering 1012bX/cm |
neutron scattering 1012bcoh/cm |
coherent cross-section σcoh (barn) |
incoherent cross-section σinc (barn) |
absorption cross-section σa (barn) |
|---|---|---|---|---|---|---|---|
| Hydrogen | 1 | 1 | 0.282[2][5] | -0.374[1][2][5][6] | 1.758[1] | 79.7,[6] 80.27[1] | 0.33,[6] 0.383[1] |
| Hydrogen | 1 | 2 | 0.282[2][5] | 0.667[1][2][5][6] | 5.592[1] | 2.0,[6] 2.05[1] | 0.0005[1][6] |
| Boron | 5 | natural | 0.530[1] | 3.54[1] | 1.70[1] | 767.0[1] | |
| Carbon | 6 | 12 | 1.69[2][5] | 0.665[1][2][5][6] | 5.550[1] | 0.0,[6] 0.001[1] | 0.0035,[6] 0.004[1] |
| Nitrogen | 7 | 14 | 1.97[2][5] | 0.936,[1] 0.940,[2] 0.94[5][6] | 11.01[1] | 0.3,[6] 0.5[1] | 1.9[1][6] |
| Oxygen | 8 | 16 | 2.16,[2] 2.26[5] | 0.580,[2] 0.58[1][5][6] | 4.232[1] | 0.0,[6] 0.000[1] | 0.00019,[6] 0.0002[1] |
| Aluminum | 13 | natural | 0.345,[1] 0.35[6] | 1.495[1] | 0.0,[6] 0.008[1] | 0.23,[6] 0.231[1] | |
| Silicon | 14 | natural | 0.42[6][7] | 0.0[6] | 0.17[6] | ||
| Phosphorus | 15 | 30 | 3.23[2] | 0.510[2] | |||
| Sulfur | 16 | 32 | 4.51[2][5] | 0.280,[2] 0.28[5] | |||
| Titanium | 22 | natural | -0.344,[1] -0.34[6][7] | 1.485[1] | 2.87,[1] 3.0[6] | 6.09,[1] 6.1[6] | |
| Vanadium | 23 | natural | -0.038[1][1] | 0.018[1] | 5.07[1] | 5.08[1] | |
| Chromium | 24 | natural | 0.364[1] | 1.66[1] | 1.83[1] | 3.05[1] | |
| Manganese | 25 | 55 (natural) | -0.373[1] | 1.75[1] | 0.4[1] | 13.3[1] | |
| Iron | 26 | natural | 0.945,[1] 0.95[6] | 11.22[1] | 0.4[1][6] | 2.56,[1] 2.6[6] | |
| Nickel | 28 | natural | 1.03[1] | 13.3[1] | 5.2[1] | 4.49[1] | |
| Copper | 29 | natural | 0.772[1] | 7.485[1] | 0.55[1] | 3.78[1] | |
| Zirconium | 40 | natural | 0.716,[1] 0.72[6] | 6.44[1] | 0.02,[1] 0.3[6] | 0.18,[6] 0.185[1] | |
| Niobium | 41 | 93 (natural) | 0.7054[1] | 6.253[1] | 0.0024[1] | 1.15[1] | |
| Molybdenum | 42 | natural | 0.672[1] | 5.67[1] | 0.04[1] | 2.48[1] | |
| Cadmium | 48 | natural | 0.487[1] | 3.04[1] | 3.46[1] | 2520[1] | |
| Tin | 50 | natural | 0.623[1] | 4.87[1] | 0.022[1] | 0.626[1] | |
| Cerium | 58 | natural | 0.48[6] | 0.0[6] | 0.63[6] | ||
| Gadolinium | 64 | natural | 0.65[1] | 29.3[1] | 151[1] | 49700[1] | |
| Tantalum | 73 | natural | 0.691[1] | 6.00[1] | 0.01[1] | 20.6[1] | |
| Tungsten | 74 | natural | 0.486[1] | 2.97[1] | 1.63[1] | 18.3[1] | |
| Gold | 79 | 197 | 22.3[2] | 0.760[2] | |||
| Lead | 82 | natural | 0.941[1] | 11.115[1] | 0.003[1] | 0.171[1] | |
| Thorium | 90 | 232 (natural) | 0.98[6] | 0.00[6] | 7.4[6] | ||
| Uranium | 92 | natural | 0.842[1][6] | 8.903[1] | 0.00,[6] 0.005[1] | 7.5,[6] 7.57[1] |
More comprehensive data is available from NIST[8] and Atominstitut of Vienna.[9]
Comparison to other reflectometry techniques
Although other reflectivity techniques (in particular optical reflectivity, x-ray reflectometry) operate using the same general principles, neutron measurements are advantageous in a few significant ways. Most notably, since the technique probes nuclear contrast, rather than electron density, it is more sensitive for measuring some elements, especially lighter elements (hydrogen, carbon, nitrogen, oxygen, etc.). Sensitivity to isotopes also allows contrast to be greatly (and selectively) enhanced for some systems of interest using isotopic substitution, and multiple experiments that differ only by isotopic substitution can be used to resolve the phase problem that is general to scattering techniques. Finally, neutrons are highly penetrating and typically non-perturbing: which allows for great flexibility in sample environments, and the use of delicate sample materials (e.g., biological specimens). By contrast x-ray exposure may damage some materials, and laser light can modify some materials (e.g. photoresists). Also, optical techniques may include ambiguity due to optical anisotropy (birefringence), which complementary neutron measurements can resolve. Dual polarisation interferometry is one optical method which provides analogous results to neutron reflectometry at comparable resolution although the underpinning mathematical model is somewhat simpler, i.e. it can only derive a thickness (or birefringence) for a uniform layer density.
Disadvantages of neutron reflectometry include the higher cost of the required infrastructure, the fact that some materials may become radioactive upon exposure to the beam, and insensitivity to the chemical state of constituent atoms. Moreover, the relatively lower flux and higher background of the technique (when compared to x-ray reflectivity) limit the maximum value of 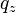 that can be probed (and hence the measurement resolution).
that can be probed (and hence the measurement resolution).
Partial list of neutron reflectometers
- ASTERIX at the Los Alamos Neutron Science Center in Los Alamos National Laboratory
- SPEAR at the Los Alamos Neutron Science Center in Los Alamos National Laboratory
- Platypus at ANSTO in Sydney, Australia
- C5 spectrometer at NRC Canada Chalk River Labs in Chalk River, Canada. Note: a new dedicated reflectometer (D3) was commissioned in 2006.
- D3 reflectometer at NRC Canada Chalk River Labs in Chalk River, Canada.
- D17, SuperADAM and Figaro at the Institut Laue-Langevin (ILL) in Grenoble, France
- EROS and PRISM (alternate) at CEA Laboratoire Léon Brillouin (LLB) in Saclay, France
- N-REX+, MIRA, TREFF@NoSpec, REFSANS and MARIA at the Forschungsneutronenquelle Heinz Maier-Leibnitz (FRM II) in Garching, Germany
- NeRo and PNR at the GKSS Research Centre (GKSS) in Geesthacht, Germany
- V6 reflectometer at Hahn-Meitner-Institut (HMI) in Berlin, Germany
- HADAS at Forschungszentrum Jülich in Jülich, Germany
- PNR at the Dhruva reactor, Bhabha Atomic Research Centre in Mumbai, India
- REFLEX and REMUR at Joint Institute for Nuclear Research IBR-2 in Dubna, Russia
- AMOR at the Paul Scherrer Institute (PSI) in Villigen, Switzerland
- SURF, CRISP, INTER, Offspec and polREF at the ISIS neutron source (ISIS) in Oxfordshire, United Kingdom
- NG1, NG7 and AND/R at the NIST Center for Neutron Research (NCNR) in Gaithersburg, Maryland, United States
- Liquids and Magnetism at the Spallation Neutron Source (ORNL) in Oak Ridge, Tennessee, United States
- Neutron Reflectometer at the University of Missouri Research Reactor, in Columbia, Missouri
A catalogue of neutron reflectometers is available at www.reflectometry.net.
Partial list of neutron reflectometry software
- Reflred and reflfit (NIST Center for Neutron Research)
- Motofit
- Parratt32 (HMI)
- Yanera (Brock University)
- StochFit
- FitSuite
- GenX
- SANGRA (web application, no local installation required)
Other neutron reflection analysis software is listed at www.reflectometry.net.
References
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 M.T. Hutchings, P.J. Withers, T.M. Holden, Torben Lorentzen (Feb 28, 2005). Introduction to the Characterization of Residual Stress by Neutron Diffraction. CRC Press.
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 Dmitri I. Svergun, Michel H. J. Koch, Peter A. Timmins, Roland P. May (Aug 8, 2013). Small Angle X-Ray and Neutron Scattering from Solutions of Biological Macromolecules. OUP Oxford.
- ↑ Amparo Lopez-Rubio and Elliot Paul Gilbert (2009). "Neutron scattering: a natural tool for food science and technology research" (PDF). Trends in Food Science & Technology: 1–11.
- ↑ Fong Shu, Venki Ramakrishnan, and Benno P. Schoenborn. "Enhanced visibility of hydrogen atoms by neutron crystallography on fully deuterated myoglobin". PNAS 97 (8): 3872–3877. doi:10.1073/pnas.060024697.
- 1 2 3 4 5 6 7 8 9 10 11 12 Oliver C. Mullins, Eric Y. Sheu, eds. (Nov 11, 2013). Structures and Dynamics of Asphaltenes. Springer Science & Business Media. p. 161.
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 N.K. Kanellopoulos, ed. (Sep 26, 2000). Recent Advances in Gas Separation by Microporous Ceramic Membranes.
- 1 2 F. Rodríguez-Reinoso, Jean Rouquerol, KK Unger, Kenneth S.W. Sing, eds. (Aug 26, 1994). Characterization of Porous Solids III. Elsevier.
- ↑ "Index of /resources/n-lengths/elements".
- ↑ "Neutron Scattering Lengths".