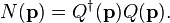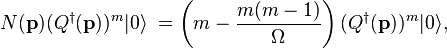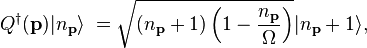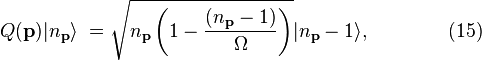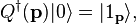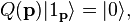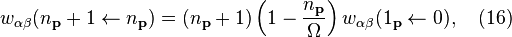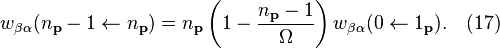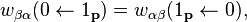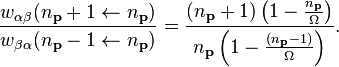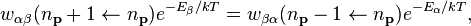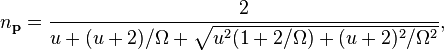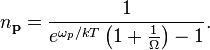Neutrino theory of light
The neutrino theory of light is the proposal that the photon is a composite particle formed of a neutrino–antineutrino pair. It is based on the idea that emission and absorption of a photon corresponds to the creation and annihilation of a particle–antiparticle pair. The neutrino theory of light is not currently accepted as part of mainstream physics, as according to the standard model the photon is an elementary particle, a gauge boson.
History
In the past, many particles that were once thought to be elementary such as protons, neutrons, pions, and kaons have turned out to be composite particles. In 1932, Louis de Broglie[1][2] suggested that the photon might be the combination of a neutrino and an antineutrino. During the 1930s there was great interest in the neutrino theory of light and Pascual Jordan,[3] Ralph Kronig, Max Born, and others worked on the theory.
In 1938, Maurice Henry Lecorney Pryce[4] brought work on the composite photon theory to halt. He showed that the conditions imposed by Bose–Einstein commutation relations for the composite photon and the connection between its spin and polarization were incompatible. Pryce also pointed out other possible problems, “In so far as the failure of the theory can be traced to any one cause it is fair to say that it lies in the fact that light waves are polarized transversely while neutrino ‘waves’ are polarized longitudinally,” and lack of rotational invariance. In 1966, V S Berezinskii[5] reanalyzed Pryce’s paper, giving a clearer picture of the problem that Pryce uncovered.
Starting in the 1960s work on the neutrino theory of light resumed, and there continues to be some interest in recent years.[6][7][8][9] Attempts have been made to solve the problem pointed out by Pryce, known as Pryce’s Theorem, and other problems with the composite photon theory. The incentive is seeing the natural way that many photon properties are generated from the theory and the knowledge that some problems exist[10][11] with the current photon model. However, there is no experimental evidence that the photon has a composite structure.
Some of the problems for the neutrino theory of light are the non-existence for massless neutrinos[12] with both spin parallel and antiparallel to their momentum and the fact that composite photons are not bosons. Attempts to solve some of these problems will be discussed, but the lack of massless neutrinos makes it impossible to form a massless photon with this theory. The neutrino theory of light is not considered to be part of mainstream physics.
Forming photon from neutrinos
Actually, it is not difficult to obtain transversely polarized photons from neutrinos.[13][14]
The neutrino field
The neutrino field satisfies the Dirac equation with the mass set to zero,
The gamma matrices in the Weyl basis are:
The matrix 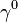 is Hermitian while
is Hermitian while 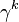 is antihermitian. They satisfy the anticommutation relation,
is antihermitian. They satisfy the anticommutation relation,
where 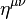 is the Minkowski metric with signature
is the Minkowski metric with signature 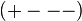 and
and  is the unit matrix.
is the unit matrix.
The neutrino field is given by,
where 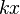 stands for
stands for 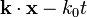 .
.
 and
and 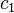 are the fermion annihilation operators for
are the fermion annihilation operators for 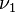 and
and 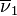 respectively, while
respectively, while  and
and 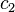 are
the annihilation operators for
are
the annihilation operators for  and
and 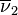 .
.
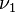 is a right-handed neutrino and
is a right-handed neutrino and  is a left-handed neutrino.
The
is a left-handed neutrino.
The 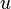 's are spinors with the superscripts and subscripts referring to the energy and helicity states respectively. Spinor solutions for the Dirac equation are,
's are spinors with the superscripts and subscripts referring to the energy and helicity states respectively. Spinor solutions for the Dirac equation are,
The neutrino spinors for negative momenta are related to those of positive momenta by,
The composite photon field
De Broglie[1] and Kronig[13] suggested the use of a local interaction to bind the neutrino–antineutrino pair. (Rosen and Singer[15] have used a delta potential interaction in forming a composite photon.) Fermi and Yang[16] used a local interaction to bind a fermion–antiferminon pair in attempting to form a pion. A four-vector field can be created from a fermion–antifermion pair,[17]
Forming the photon field can be done simply by,
where 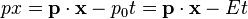 .
.
The annihilation operators for right-handed and left-handed photons formed of fermion–antifermion pairs are defined as,[18][19][20][21]
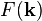 is a spectral function, normalized by
is a spectral function, normalized by
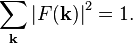
Photon polarization vectors
The polarization vectors corresponding to the combinations used in Eq. (1) are,
Carrying out the matrix multiplications results in,
where 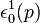 and
and 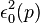 have been placed on the right.
have been placed on the right.
For massless fermions the polarization vectors depend only upon the direction of
 . Let
. Let 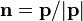 .
.
These polarization vectors satisfy the normalization relation,
The Lorentz-invariant dot
products of the internal four-momentum 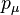 with the polarization vectors are,
with the polarization vectors are,
In three dimensions,
Composite photon satisfies Maxwell’s equations
In terms of the polarization vectors, 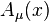 becomes,
becomes,
The electric field 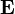 and magnetic field
and magnetic field
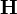 are given by,
are given by,
Applying Eq. (6) to Eq. (5), results in,
Maxwell's equations for free space are obtained as follows:
Thus, 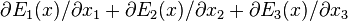 contains terms of the form
contains terms of the form
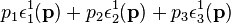 which equate to zero by the first of Eq. (4).
This gives,
which equate to zero by the first of Eq. (4).
This gives,
as  contains similar terms.
contains similar terms.
The expression 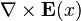 contains terms of the form
contains terms of the form
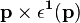 while
while
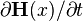 contains terms of form
contains terms of form 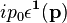 . Thus, the last two equations of (4) can be used to show that,
. Thus, the last two equations of (4) can be used to show that,
Although the neutrino field violates parity and charge
conjugation
,[22]
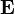 and
and
 transform in the usual way
,[14][21]
transform in the usual way
,[14][21]
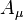 satisfies the Lorenz condition,
satisfies the Lorenz condition,
which follows from Eq. (3).
Although many choices for gamma matrices can satisfy the Dirac equation, it
is essential that one use the Weyl representation in order to get the correct photon polarization vectors and 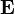 and
and  that satisfy Maxwell's equations. Kronig[13]
first realized this. In the Weyl representation,
the four-component spinors are describing two sets of two-component neutrinos.
The connection between the photon antisymmetric tensor and the two-component Weyl equation was also noted by Sen.[23]
One can also produce the above results using a two-component neutrino theory.[8]
that satisfy Maxwell's equations. Kronig[13]
first realized this. In the Weyl representation,
the four-component spinors are describing two sets of two-component neutrinos.
The connection between the photon antisymmetric tensor and the two-component Weyl equation was also noted by Sen.[23]
One can also produce the above results using a two-component neutrino theory.[8]
To compute the commutation relations for the photon field, one needs the equation,
To obtain this equation, Kronig[13] wrote a relation between the neutrino spinors that was not rotationally invariant as pointed out by Pryce.[4] However, as Perkins[14] showed, this equation follows directly from summing over the polarization vectors, Eq. (2), that were obtained by explicitly solving for the neutrino spinors.
If the momentum is along the third axis, 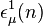 and
and 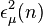 reduce to the usual polarization vectors
for right and left circularly polarized photons respectively.
reduce to the usual polarization vectors
for right and left circularly polarized photons respectively.
Problems with the neutrino theory of light
Although composite photons satisfy many properties of real photons, there are major problems with this theory.
Bose–Einstein commutation relations
It is known that a photon is a boson.[24] Does the composite photon satisfy Bose–Einstein commutation relations? Fermions are defined as the particles whose creation and annihilation operators adhere to the anticommutation relations
while bosons are defined as the particles that adhere to the commutation relations
The creation and annihilation operators of composite particles formed of fermion pairs adhere to the commutation relations of the form[18][19][20][21]
with
For Cooper electron pairs,[20] "a" and "c" represent different spin directions. For nucleon pairs (the deuteron),[18][19] "a" and "c" represent proton and neutron. For neutrino–antineutrino pairs,[21] "a" and "c" represent neutrino and antineutrino. The size of the deviations from pure Bose behavior,
depends on the degree of overlap of the fermion wave functions and the constraints of the Pauli exclusion principle.
If the state has the form
then the expectation value of Eq. (9) vanishes for 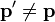 , and the expression for
, and the expression for
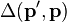 can be approximated by
can be approximated by
Using the fermion number operators 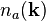 and
and 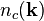 , this can be written,
, this can be written,
showing that it is the average number
of fermions in a particular state  averaged
over all states with weighting factors
averaged
over all states with weighting factors 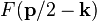 and
and 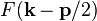 .
.
Jordan’s attempt to solve problem
De Broglie did not address the problem of statistics for the composite photon. However, "Jordan considered the essential part of the problem was to construct Bose–Einstein amplitudes from Fermi–Dirac amplitudes", as Pryce[4] noted. Jordan[3] "suggested that it is not the interaction between neutrinos and antineutrinos that binds them together into photons, but rather the manner in which they interact with charged particles that leads to the simplified description of light in terms of photons."
Jordan's hypothesis eliminated the need for theorizing an unknown interaction, but his hypothesis that the neutrino and antineutrino are emitted in exactly the same direction seems rather artificial as noted by Fock.[25] His strong desire to obtain exact Bose–Einstein commutation relations for the composite photon led him to work with a scalar or longitudinally polarized photon. Greenberg and Wightman[26] have pointed out why the one-dimensional case works, but the three-dimensional case does not.
In 1928, Jordan noticed that commutation relations for
pairs of fermions were similar to those for bosons.[27]
Compare Eq. (7) with Eq. (8).
From 1935 till 1937, Jordan, Kronig, and others[28]
tried to obtain exact Bose–Einstein commutation relations for the composite photon. Terms were added to the commutation relations to cancel out the delta term in Eq. (8). These terms corresponded to "simulated photons". For example, the absorption of a photon of momentum  could be simulated by a Raman effect in which a neutrino with momentum
could be simulated by a Raman effect in which a neutrino with momentum 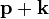 is absorbed while another of another with opposite spin and momentum
is absorbed while another of another with opposite spin and momentum  is emitted. (It is now known that single neutrinos or antineutrinos interact so weakly that they cannot simulate photons.)
is emitted. (It is now known that single neutrinos or antineutrinos interact so weakly that they cannot simulate photons.)
Pryce’s theorem
In 1938, Pryce[4] showed that one cannot obtain both Bose–Einstein statistics and transversely polarized photons from neutrino–antineutrino pairs. Construction of transversely polarized photons is not the problem.[29] As Berezinski[5] noted, "The only actual difficulty is that the construction of a transverse four-vector is incompatible with the requirement of statistics." In some ways Berezinski gives a clearer picture of the problem. A simple version of the proof is as follows:
The expectation values of the commutation relations for composite right and left-handed photons are:
where
The deviation from Bose–Einstein statistics is caused by 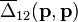 and
and
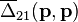 , which are functions of the neutrino numbers operators.
, which are functions of the neutrino numbers operators.
Linear polarization photon operators are defined by
A particularly interesting commutation relation is,
which follows from (10) and (12).
For the composite photon to obey Bose–Einstein commutation relations, at the very least,
Pryce noted.[4] From Eq. (11) and Eq. (13) the requirement is that
gives zero when applied to any state vector. Thus, all the coefficients of
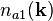 and
and 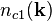 ,
etc. must vanish separately. This means
,
etc. must vanish separately. This means 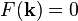 ,
and the composite photon does not exist,[4][5] completing the proof.
,
and the composite photon does not exist,[4][5] completing the proof.
Perkins’ attempt to solve problem
Perkins[14][21] reasoned that the photon does not have to obey Bose–Einstein commutation relations, because the non-Bose terms are small and they may not cause any detectable effects. Perkins[11] noted, "As presented in many quantum mechanics texts it may appear that Bose statistics follow from basic principles, but it is really from the classical canonical formalism. This is not a reliable procedure as evidenced by the fact that it gives the completely wrong result for spin-1/2 particles." Furthermore, "most integral spin particles (light mesons, strange mesons, etc.) are composite particles formed of quarks. Because of their underlying fermion structure, these integral spin particles are not fundamental bosons, but composite quasibosons. However, in the asymptotic limit, which generally applies, they are essentially bosons. For these particles, Bose commutation relations are just an approximation, albeit a very good one. There are some differences; bringing two of these composite particles close together will force their identical fermions to jump to excited states because of the Pauli exclusion principle."
Brzezinski in reaffirming Pryce's theorem argues that commutation relation (14) is necessary for the photon to be truly neutral. However, Perkins[21] has shown that a neutral photon in the usual sense can be obtained without Bose–Einstein commutation relations.
The number operator for a composite photon is defined as
Lipkin[18]
suggested for a rough estimate to assume
that 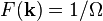 where
where  is a constant equal
to the number of states used to construct the wave packet.
is a constant equal
to the number of states used to construct the wave packet.
Perkins[11]
showed that the effect
of the composite photon’s
number operator acting on a state of  composite photons is,
composite photons is,
using 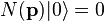 .
This result differs from the usual
one because of the second term which is small for large
.
This result differs from the usual
one because of the second term which is small for large  .
Normalizing in the
usual manner,[30]
.
Normalizing in the
usual manner,[30]
where 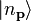 is the state of
is the state of 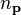 composite photons having momentum
composite photons having momentum  which is created
by applying
which is created
by applying 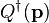 on the vacuum
on the vacuum 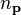 times.
Note that,
times.
Note that,
which is the same result as obtained
with boson operators. The formulas in Eq. (15)
are similar to the usual ones with correction factors
that approach zero for large  .
.
Blackbody radiation
The main evidence indicating that photons are bosons comes from the Blackbody radiation experiments which are in agreement with Planck's distribution. Perkins[11] calculated the photon distribution for Blackbody radiation using the second quantization method,[30] but with a composite photon.
The atoms in the walls of the cavity are taken to be a two-level system with photons emitted from the upper level β and absorbed at the lower level α. The transition probability for emission of a photon is enhanced when np photons are present,
where the first of (15) has been used. The absorption is enhanced less since the second of (15) is used,
Using the equality,
of the transition rates, Eqs. (16) and (17) are combined to give,
The probability of finding the system with energy E is proportional to e−E/kT according to Boltzmann's distribution law. Thus, the equilibrium between emission and absorption requires that,
with the photon energy 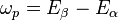 . Combining the last two equations results in,
. Combining the last two equations results in,
with 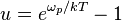 . For
. For 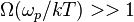 , this reduces to
, this reduces to
This equation differs from Planck’s law because of the 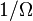 term. For the conditions used in the Blackbody radiation experiments of Coblentz,[31] Perkins estimates that 1 / Ω < 10−9, and the maximum deviation from Planck's law is less than one part in 10−8, which is too small to be detected.
term. For the conditions used in the Blackbody radiation experiments of Coblentz,[31] Perkins estimates that 1 / Ω < 10−9, and the maximum deviation from Planck's law is less than one part in 10−8, which is too small to be detected.
Only left-handed neutrinos exist
Experimental results show that only left-handed neutrinos and right-handed antineutrinos exist. Three sets of neutrinos have been observed,[32][33] one that is connected with electrons, one with muons, and one with tau leptons.[34]
In the standard model the pion and muon decay modes are:
π+ → μ+ + ν
μμ+ → e+ + ν
e+ ν
μ
To form a photon, which satisfies parity and charge conjugation, two sets of two-component neutrinos (i.e., right-handed and left-handed neutrinos) are needed. Perkins (see Sec. VI of Ref.[14]) attempted to solve this problem by noting that the needed two sets of two-component neutrinos would exist if the positive muon is identified as the particle and the negative muon as the antiparticle. The reasoning is as follows: let ν1 be the right-handed neutrino and ν2 the left-handed neutrino with their corresponding antineutrinos (with opposite helicity). The neutrinos involved in beta decay are ν2 and ν2, while those for π–μ decay are ν1 and ν1. With this scheme the pion and muon decay modes are:
π+ → μ+ + ν1 μ+ → e+ + ν2 + ν1
Absence of massless neutrinos
There is convincing evidence that neutrinos have mass. In experiments at the SuperKamiokande researchers[12] have discovered neutrino oscillations in which one flavor of neutrino changed into another. This means that neutrinos have non-zero mass. Since massless neutrinos are needed to form a massless photon, a composite photon is not possible.
References
- 1 2 L. de Broglie (1932). Compt. Rend. 195: 536, 862. Missing or empty
|title=(help) - ↑ L. de Broglie (1934). Une novelle conception de la lumiere. Paris (France): Hermann et. Cie.
- 1 2 P. Jordan (1935). "Zur Neutrinotheorie des Lichtes". Z. Phys. 93 (7–8): 464–472. Bibcode:1935ZPhy...93..464J. doi:10.1007/BF01330373.
- 1 2 3 4 5 6 M. H. L. Pryce (1938). "On the neutrino theory of light". Proceedings of the Royal Society A165: 247–271.
- 1 2 3 V. S. Berezinskii (1966). "Pryce's theorem and the neutrino theory of photons". Zh. Eksperim. I Teor. Fiz. 51: 1374–1384.
- translated in Soviet Physics JETP, 24: 927 (1967)
- ↑ V. V. Dvoeglazov (1999). "Speculations on the neutrino theory of light". Annales Fond. Broglie 24: 111–127. arXiv:physics/9807013. Bibcode:1998physics...7013D.
- ↑ V. V. Dvoeglazov (2001). "Again on the possible compositeness of the photon". Phys. Scripta 64 (2): 119–127. arXiv:hep-th/9908057. Bibcode:2001PhyS...64..119D. doi:10.1238/Physica.Regular.064a00119.
- 1 2 W. A. Perkins (1999). "Interpreted History of Neutrino Theory of Light and Its Future". In A. E. Chubykalo, V. V. Dvoeglazov, D. J. Ernst, V. G. Kadyshevsky, and Y. S. Kim. Lorentz Group, CPT and Neutrinos: Proceedings of the International Workshop, Zacatecas, Mexico, 23-26 June 1999. pp. 115–126.
- ↑ D. K. Sen (2007). "Left- and right-handed neutrinos and baryon–lepton masses". Journal of Mathematical Physics 48 (2): 022304. Bibcode:2007JMP....48b2304S. doi:10.1063/1.2436985.
- ↑ V. V. Varlamov (2001). "About Algebraic Foundation of Majorana–Oppenheimer Quantum Electrodynamics and de Brogie–Jordan Neutrino Theory of Light". arXiv:math-ph/0109024.
- 1 2 3 4 W. A. Perkins (2002). "Quasibosons". International Journal of Theoretical Physics 41 (5): 823–838. doi:10.1023/A:1015728722664.
- 1 2 Y. Fukuda et al. (Super-Kamiokande Collaboration) (1998). "Evidence for oscillation of atmospheric neutrinos". Physical Review Letters 81 (8): 1562–1567. arXiv:hep-ex/9807003. Bibcode:1998PhRvL..81.1562F. doi:10.1103/PhysRevLett.81.1562.
- 1 2 3 4 R. de L. Kronig (1936). "On a relativistically invariant formulation of the neutrino theory of light". Physica 3 (10): 1120–1132. Bibcode:1936Phy.....3.1120K. doi:10.1016/S0031-8914(36)80340-1.
- 1 2 3 4 5 W. A. Perkins (1965). "Neutrino theory of photons". Physical Review 137 (5B): B1291–B1301. Bibcode:1965PhRv..137.1291P. doi:10.1103/PhysRev.137.B1291.
- ↑ N. Rosen and P. Singer (1959). "The photon as a composite particle". Bulletin of the Research Council of Israel 8F (5): 51–62. Bibcode:1967PhRv..157.1444B. doi:10.1103/PhysRev.157.1444.
- ↑ E. Fermi and C. N. Yang (1949). "Are mesons elementary particles". Physical Review 76 (12): 1739–1743. Bibcode:1949PhRv...76.1739F. doi:10.1103/PhysRev.76.1739.
- ↑ J. D. Bjorken and S. D. Drell (1965). Relativistic Quantum Fields. New York (NY): McGraw-Hill.
- 1 2 3 4 H. J. Lipkin (1973). Quantum Mechanics. Amsterdam (Netherlands): North-Holland.
- 1 2 3 H. L. Sahlin and J. L. Schwartz (1965). "The many body problem for composite particles". Physical Review 138: B267–B273. Bibcode:1965PhRv..138..267S. doi:10.1103/PhysRev.138.B267.
- 1 2 3 R. H. Landau (1996). Quantum Mechanics II. New York (NY): Wiley.
- 1 2 3 4 5 6 W. A. Perkins (1972). "Statistics of a composite photon formed of two fermions". Physical Review D 5 (6): 1375–1384. Bibcode:1972PhRvD...5.1375P. doi:10.1103/PhysRevD.5.1375.
- ↑ T. D. Lee and C. N. Yang (1957). "Parity nonconservation and two-component theory of the neutrino". Physical Review 105 (5): 1671–1675. Bibcode:1957PhRv..105.1671L. doi:10.1103/PhysRev.105.1671.
- ↑ D. K. Sen (1964). "A theoretical basis for two neutrinos". Il Nuovo Cimento 31 (3): 660–669. doi:10.1007/BF02733763.
- ↑ C. Amsler et al. (Particle Data Group) (2008). "The review of particle physics". Physics Letters B 667: 1–1340. Bibcode:2008PhLB..667....1P. doi:10.1016/j.physletb.2008.07.018.
- ↑ Fock (1937). Phys. Z. Sowjetunion 11: 1. Missing or empty
|title=(help) - ↑ O. W. Greenberg and A. S. Wightman (1955). "Re-examination of the neutrino theory of light". Physical Review 99: 675 A. Bibcode:1955PhRv...99..605.. doi:10.1103/PhysRev.99.605.
- ↑ P. Jordan (1928). "Die Lichtquantenhypothese: Entwicklung und gegenwärtiger Stand". Ergebnisse der exakten Naturwissenschaften 7: 158–208. Bibcode:1928ErNW....7..158J. doi:10.1007/BFb0111850.
- ↑ M. Born and N. S. Nagendra Nath (1936). Proc. Indian Acad. Sci. A3: 318. Missing or empty
|title=(help) - ↑ K. M. Case (1957). "Composite particles of zero mass". Physical Review 106 (6): 1316–1320. Bibcode:1957PhRv..106.1316C. doi:10.1103/PhysRev.106.1316.
- 1 2 D. S. Koltun and J. M. Eisenberg (1988). Quantum Mechanics of Many Degrees of Freedom. New York (NY): Wiley.
- ↑ W. W. Coblentz (1916). Natl. Bur. Std. (U.S.) Bull. 13: 459. doi:10.6028/bulletin.310. Missing or empty
|title=(help) - ↑ G. Danby, J-M Gaillard, K. Goulianos, L. M. Lederman,
N. Mistry, M. Schwartz, and J. Steinberger, (1962). "Observation of high-energy neutrino interactions and the existence of two kinds of neutrinos". Physical Review Letters 9: 36–44. Bibcode:1962PhRvL...9...36D. doi:10.1103/PhysRevLett.9.36. line feed character in
|author=at position 54 (help) - ↑ K. Kodama et al. (DONUT collaboration) (2001). "Observation of tau neutrino interactions". Physics Letters B 504 (3): 218–224. arXiv:hep-ex/0012035. Bibcode:2001PhLB..504..218D. doi:10.1016/S0370-2693(01)00307-0.
- ↑ M. L. Perl; et al. (1975). "Evidence for anomalous lepton production in e+ – e− annihilation". Physical Review Letters 35 (22): 1489–1492. Bibcode:1975PhRvL..35.1489P. doi:10.1103/PhysRevLett.35.1489.
External links
- L. de Broglie "A new conception of light" (English translation)
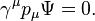
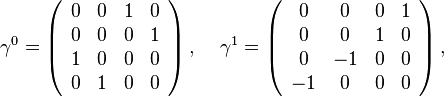
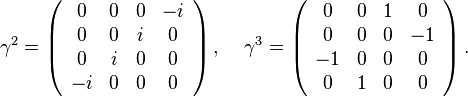
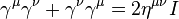
![\Psi(x) = {1 \over \sqrt{V}} \sum_\mathbf{k} \left\{
\left[ a_1(\mathbf{k}) u^{+1}_{+1}(\mathbf{k}) + a_2(\mathbf{k}) u^{+1}_{-1}(\mathbf{k})
\right] e^{i k x} \right.](../I/m/119f7c6c8d5c7e79290b877fa89e25de.png)
![\left. + \left[ c_1^\dagger(\mathbf{k}) u^{-1}_{-1} (\mathbf{-k})
+ c_2^\dagger(\mathbf{k}) u^{-1}_{+1}(\mathbf{-k}) \right]e^{-i k x} \right\},](../I/m/3c164bb5a38bcbbbf0c5a4df400f628c.png)
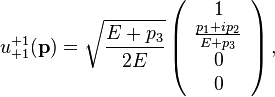
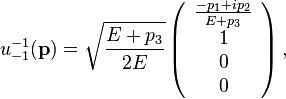
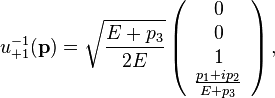
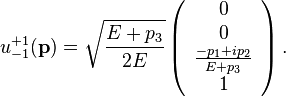
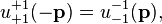
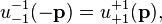
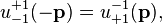

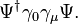
![A_\mu(x) = \sum_\mathbf{p} {-1 \over 2 \sqrt{V p_0}}\left\{
\left[Q_R(\mathbf{p}) u^{-1}_{-1}(\mathbf{p})^\dagger \gamma_0 \gamma_{\mu} u^{+1}_{+1}(\mathbf{p})
+ Q_L(\mathbf{p}) u^{+1}_{+1}(\mathbf{p})^\dagger \gamma_0 \gamma_{\mu}
u^{-1}_{-1}(\mathbf{p}) \right]e^{i p x}
\right.](../I/m/121c94da4ae042d8239a7c1b97d0aa58.png)
![\left. + \left[Q_R^\dagger(\mathbf{p}) u^{+1}_{+1}(\mathbf{p})^\dagger \gamma_0 \gamma_{\mu} u^{-1}_{-1}(\mathbf{p})
+ Q_L^\dagger(\mathbf{p}) u^{-1}_{-1}(\mathbf{p})^\dagger \gamma_0 \gamma_{\mu} u^{+1}_{+1}(\mathbf{p})
\right]e^{-i p x} \right\}, \quad\quad (1)](../I/m/552c6e25f806f387f4762e9735395470.png)
![Q_R(\mathbf{p}) = \sum_\mathbf{k} F^\dagger(\mathbf{k})
\left [ c_1(\mathbf{p}/2-\mathbf{k})a_1(\mathbf{p}/2+\mathbf{k})
+ c_2(\mathbf{p}/2+\mathbf{k})a_2(\mathbf{p}/2-\mathbf{k}) \right ]](../I/m/7918d2231549686399d94333774008d4.png)
![Q_L(\mathbf{p}) = \sum_\mathbf{k} F^\dagger(\mathbf{k})
\left [ c_2(\mathbf{p}/2-\mathbf{k})a_2(\mathbf{p}/2+\mathbf{k})
+ c_1(\mathbf{p}/2+\mathbf{k})a_1(\mathbf{p}/2-\mathbf{k}), \right ].](../I/m/4dba35121ac9e4c1a011ff08819b494a.png)
![\epsilon_\mu^1( p ) = {-1 \over \sqrt{2}} [u^{-1}_{-1}(\mathbf{p})]^\dagger
\gamma_0 \gamma_{\mu} u^{+1}_{+1}(\mathbf{p}),](../I/m/47221769c846fa6de5c9b02c17fa03ea.png)
![\epsilon_\mu^2( p ) = {-1 \over \sqrt{2}} [u^{+1}_{+1}(\mathbf{p})]^\dagger
\gamma_0 \gamma_{\mu} u^{-1}_{-1}(\mathbf{p}).](../I/m/89377e732bfa3a0893b0b8a47b35d502.png)
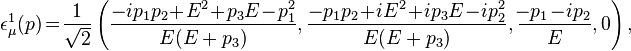
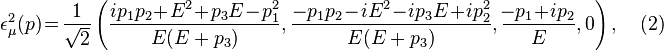
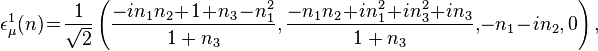
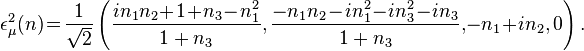
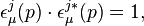
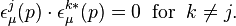
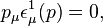
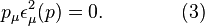
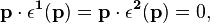
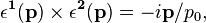
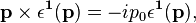
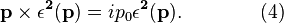
![A_\mu(x) = \sum_\mathbf{p} {1 \over \sqrt{2 V p_0}}\left\{
\left[Q_R(\mathbf{p}) \epsilon_\mu^1(\mathbf{p}) + Q_L(\mathbf{p})
\epsilon_\mu^2(\mathbf{p})
\right]e^{i p x} \right.](../I/m/8ae1385013e2a2f4303d4ca7c36f19bc.png)
![\left. + \left[Q_R^\dagger(\mathbf{p}) \epsilon_\mu^{1*}(\mathbf{p})
+ Q_L^\dagger(\mathbf{p}) \epsilon_\mu^{2*}(\mathbf{p})
\right]e^{-i p x} \right\}. \quad\quad\quad (5)](../I/m/eddad7d482ef83838de70a70e57a2453.png)
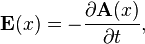
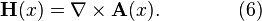
![E_\mu(x) = i \sum_\mathbf{p} {\sqrt{p_0} \over \sqrt{2 V }}\left\{
\left[Q_R(\mathbf{p}) \epsilon_\mu^1(\mathbf{p})
+ Q_L(\mathbf{p}) \epsilon_\mu^2(\mathbf{p}) \right]e^{i p x}
\right.](../I/m/6399558dc5cb631e64f5dad7565f4d23.png)
![\left. - \left[Q_R^\dagger(\mathbf{p}) \epsilon_\mu^{1*}(\mathbf{p})
+ Q_L^\dagger(\mathbf{p}) \epsilon_\mu^{2*}(\mathbf{p}),
\right]e^{-i p x} \right\}.](../I/m/b94f0051afe107209efca47a571540a0.png)
![H_\mu(x) = \sum_\mathbf{p} {\sqrt{p_0} \over \sqrt{2 V }}\left\{
\left[Q_R(\mathbf{p}) \epsilon_\mu^1(\mathbf{p})
- Q_L(\mathbf{p}) \epsilon_\mu^2(\mathbf{p}) \right]e^{i p x}
\right.](../I/m/87d52ec4ab93d6bed9dd1e63088eebb7.png)
![\left. + \left[Q_R^\dagger(\mathbf{p}) \epsilon_\mu^{1*}(\mathbf{p})
- Q_L^\dagger(\mathbf{p}) \epsilon_\mu^{2*}(\mathbf{p}),
\right]e^{-i p x} \right\}.](../I/m/a02e2c0f01b77e2f779b60cc12da782e.png)
![\partial E_1(x) / \partial x_1 =
i \sum_\mathbf{p} {\sqrt{p_0} \over \sqrt{2 V }}\left\{
\left[Q_R(\mathbf{p}) p_1 \epsilon_1^1(\mathbf{p})
+ Q_L(\mathbf{p}) p_1 \epsilon_1^2(\mathbf{p}) \right]e^{i p x}
\right.](../I/m/165d244f745f66b49a432e1547349bee.png)
![\left. + \left[Q_R^\dagger(\mathbf{p}) p_1 \epsilon_1^{1*}(\mathbf{p})
+ Q_L^\dagger(\mathbf{p}) p_1 \epsilon_1^{2*}(\mathbf{p})
\right]e^{-i p x} \right\}.](../I/m/6a12bd235e1a0514b240168d82ec31e2.png)
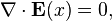
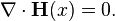
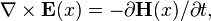
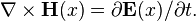
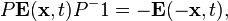
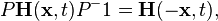
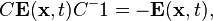
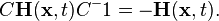
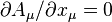
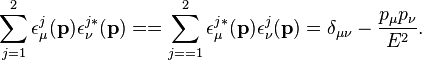
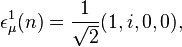
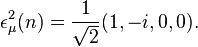
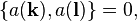
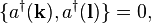
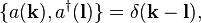
![\left[b(\mathbf{k}),b(\mathbf{l})\right] = 0,](../I/m/9821d933cea2394c41c4a5495b6026d9.png)
![\left[b^\dagger(\mathbf{k}),b^\dagger(\mathbf{l})\right] = 0,](../I/m/66176f17c23ba962159bd0c9a8e6e543.png)
![\left[b(\mathbf{k}),b^\dagger(\mathbf{l})\right]
= \delta(\mathbf{k}-\mathbf{l}). \quad\quad (7)](../I/m/01232ea0e76da4fdf1a79724941d20ec.png)
![\left[Q(\mathbf{k}),Q(\mathbf{l})\right] = 0,](../I/m/3317f2191e4cfd514c366f0a1d1bafb9.png)
![\left[Q^\dagger(\mathbf{k}),Q^\dagger(\mathbf{l})\right] = 0,](../I/m/7d2b0553025756f2e85583876d3dcb56.png)
![\left[Q(\mathbf{k}),Q^\dagger(\mathbf{l})\right]
= \delta(\mathbf{k}-\mathbf{l})- \Delta(\mathbf{k},\mathbf{l}). \quad\quad (8)](../I/m/c19471dfde67b338cb7bcd241a71efeb.png)
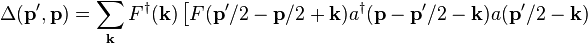
![\left.
+ F(\mathbf{p}/2-\mathbf{p}^{\prime}/2+\mathbf{k})
c^\dagger(\mathbf{p}-\mathbf{p}^{\prime}/2+\mathbf{k})
c(\mathbf{p}^{\prime}/2+\mathbf{k}) \right]. \quad\quad (9)](../I/m/b7b84e54b4ee0aa93ac7a9e5339311d7.png)
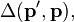
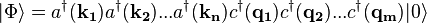
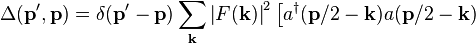
![\left.
+ c^\dagger(\mathbf{p}/2+\mathbf{k})
c(\mathbf{p}/2+\mathbf{k}) \right].](../I/m/b0b031de750d72a0ad26452207ec70f9.png)
![\Delta(\mathbf{p}^{\prime},\mathbf{p}) =
\delta(\mathbf{p}^{\prime}-\mathbf{p})
\sum_\mathbf{k} \left| F(\mathbf{k}) \right|^2
\left[ n_a( \mathbf{p}/2-\mathbf{k})
+ n_c(\mathbf{p}/2+\mathbf{k})
\right]](../I/m/9e380419258ca4b00030cc279338ea45.png)
![= \delta(\mathbf{p}^{\prime}-\mathbf{p})
\sum_\mathbf{k} \left[ \left| F(\mathbf{p}/2-\mathbf{k}) \right|^2
n_a(\mathbf{k}) + \left| F(\mathbf{k}- \mathbf{p}/2) \right|^2
n_c(\mathbf{k}) \right]](../I/m/598c354879323218ffcb2d00d5956c58.png)
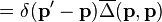
![\left[ Q_R(\mathbf{p}^{\prime}),
Q_R(\mathbf{p}) \right] = 0, \;
\left[ Q_L(\mathbf{p}^{\prime}),
Q_L(\mathbf{p}) \right] = 0,](../I/m/02ce96b1222e12d127f8f824ba5431ab.png)
![\left[ Q_R(\mathbf{p}^{\prime}),
Q_R^\dagger(\mathbf{p}) \right]
= \delta( \mathbf{p}^{\prime} - \mathbf{p})
(1 -{\overline \Delta_{12}}(\mathbf{p},\mathbf{p})),](../I/m/9ed9911e9f1d4ba929d846194053f2e0.png)
![\left[ Q_L(\mathbf{p}^{\prime}),
Q_L^\dagger(\mathbf{p}) \right]
= \delta( \mathbf{p}^{\prime} - \mathbf{p})
(1 -{\overline \Delta_{21}}(\mathbf{p},\mathbf{p})),](../I/m/f0e3c5d2789622e9aaf8b5532fd87a76.png)
![\left[ Q_R(\mathbf{p}^{\prime}),
Q_L(\mathbf{p}) \right] = 0, \;
\left[ Q_R(\mathbf{p}^{\prime}),
Q_L^\dagger(\mathbf{p}) \right] = 0, \quad\quad\quad\quad (10)](../I/m/c8f0521aa7e370817ea9f4ea0543bae8.png)
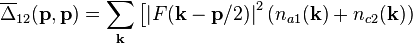
![\left.
+ \left| F(\mathbf{p}/2-\mathbf{k}) \right|^2 ( n_{c1}(\mathbf{k}) + n_{a2}(\mathbf{k}) )
\right]. \quad\quad\quad\quad (11)](../I/m/432eaba6d71871ccbb2e84d533968ed5.png)
![\xi( \mathbf{p}) = {1 \over \sqrt{2}} \left[ Q_L(\mathbf{p})
+ Q_R(\mathbf{p}) \right],](../I/m/c536eb0311452e26fa202624a6078c97.png)
![\eta( \mathbf{p}) = {i \over \sqrt{2}} \left[ Q_L(\mathbf{p})
- Q_R(\mathbf{p}) \right]. \quad\quad\quad\quad (12)](../I/m/ee78684299603645e3b317ba0e6fe949.png)
![[\xi( \mathbf{p}^{\prime}),\eta^\dagger( \mathbf{p})]
= {i \over 2} \delta( \mathbf{p}^{\prime} - \mathbf{p})
[\overline \Delta_{21}(\mathbf{p},\mathbf{p})
-\overline \Delta_{12}(\mathbf{p},\mathbf{p})], \quad\quad (13)](../I/m/909fc769c7662c770e92bfca28784a00.png)
![[\xi( \mathbf{p}^{\prime}),\eta^\dagger( \mathbf{p})]
= 0 \quad\quad\quad\quad (14)](../I/m/2f517cd1d1db5843a49fc5a9b6ef46d4.png)
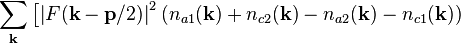
![\left. + \left| F(\mathbf{p}/2-\mathbf{k}) \right|^2
( n_{c1}(\mathbf{k}) + n_{a2}(\mathbf{k}) - n_{c2}(\mathbf{k}) - n_{a1}(\mathbf{k}) )
\right]](../I/m/f66d05933e6ae962a5e474e5d751a539.png)