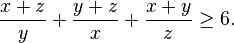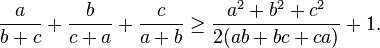Nesbitt's inequality
In mathematics, Nesbitt's inequality is a special case of the Shapiro inequality. It states that for positive real numbers a, b and c we have:
Proof
First proof: AM-HM
Clearing denominators yields
from which we obtain
by expanding the product and collecting like denominators. This then simplifies directly to the final result.
Second proof: Rearrangement
Suppose  , we have that
, we have that
define
The scalar product of the two sequences is maximum because of the rearrangement inequality if they are arranged the same way, call 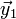 and
and  the vector
the vector  shifted by one and by two, we have:
shifted by one and by two, we have:
Addition yields Nesbitt's inequality.
Third proof: Hilbert's Seventeenth Problem
The following identity is true for all 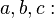
This clearly proves that the left side is no less than  for positive a,b and c.
for positive a,b and c.
Note: every rational inequality can be solved by transforming it to the appropriate identity, see Hilbert's seventeenth problem.
Fourth proof: Cauchy–Schwarz
Invoking the Cauchy–Schwarz inequality on the vectors  yields
yields
which can be transformed into the final result as we did in the AM-HM proof.
Fifth proof: AM-GM
We first employ a Ravi substitution: let  . We then apply the AM-GM inequality to the set of six values
. We then apply the AM-GM inequality to the set of six values  to obtain
to obtain
Dividing by  yields
yields
Substituting out the  in favor of
in favor of 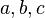 yields
yields
which then simplifies directly to the final result.
Sixth proof: Titu's lemma
Titu's lemma, a direct consequence of the Cauchy–Schwarz inequality, states that for any sequence of  real numbers
real numbers  and any sequence of
and any sequence of  positive numbers
positive numbers  ,
,  . We use its three-term instance with
. We use its three-term instance with  -sequence
-sequence 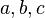 and
and  -sequence
-sequence  :
:
By multiplying out all the products on the lesser side and collecting like terms, we obtain
which simplifies to
By the rearrangement inequality, we have  , so the fraction on the lesser side must be at least
, so the fraction on the lesser side must be at least  . Thus,
. Thus,
References
- Arthur Lohwater (1982). "Introduction to Inequalities". Online e-book in PDF format.
External links
- See AoPS for more proofs of this inequality.
- Nesbitt's inequality at PlanetMath.org.
- proof of Nesbitt's inequality at PlanetMath.org.

 ,
,



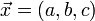





![\frac{\left(x^2z+z^2x\right)+\left(y^2z+z^2y\right)+\left(x^2y+y^2x\right)}{6}\geq\sqrt[6]{x^2z\cdot z^2x\cdot y^2z\cdot z^2y\cdot x^2y\cdot y^2x}=xyz.](../I/m/dc047802d4576ebf8b9b406ac8c2b006.png)