Negative hypergeometric distribution
| Parameters |
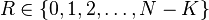 - number of failures when experiment is stopped - number of failures when experiment is stopped |
|---|---|
| Support |
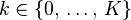 - number of successes when experiment is stopped. - number of successes when experiment is stopped. |
| Mean |
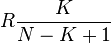 |
| Variance |
![R\frac{(N+1)K}{(N-K+1)(N-K+2)}[1-\frac{R}{N-K+1}]](../I/m/dd2a6e95a71a96a509e93834c940d45e.png) |
In probability theory and statistics, the negative hypergeometric distribution describes probabilities for when sampling from a finite population without replacement in which each sample can be classified into two mutually exclusive categories like Pass/Fail, Male/Female or Employed/Unemployed. As random selections are made from the population, each subsequent draw decreases the population causing the probability of success to change with each draw. Unlike the standard hypergeometric distribution, which describes the number of successes in a fixed sample size, in the negative hypergeometric distribution, samples are drawn until  failures have been found, and the distribution describes the probability of finding
failures have been found, and the distribution describes the probability of finding  successes in such a sample. In other words, the negative hypergeometric distribution describes the likelihood of
successes in such a sample. In other words, the negative hypergeometric distribution describes the likelihood of  successes in a sample with exactly
successes in a sample with exactly  failures.
failures.
Definition
There are  elements, of which
elements, of which  are defined as "successes" and the rest are "failures".
are defined as "successes" and the rest are "failures".
Elements are drawn one after the other, without replacements, until  failures are encountered. Then, the drawing stops and the number
failures are encountered. Then, the drawing stops and the number  of successes is counted. The negative hypergeometric distribution,
of successes is counted. The negative hypergeometric distribution, 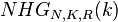 is the discrete distribution of this
is the discrete distribution of this  .
.
Related distributions
If the drawing stops after a constant number  of draws (regardless of the number of failures), then the number of successes has the hypergeometric distribution,
of draws (regardless of the number of failures), then the number of successes has the hypergeometric distribution, 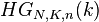 . The two functions are related in the following way:[1]
. The two functions are related in the following way:[1]
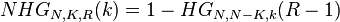
Negative-hypergeometric distribution (like the hypergeometric distribution) deals with draws without replacement, so that the probability of success is different in each draw. In contrast, negative-binomial distribution (like the binomial distribution) deals with draws with replacement, so that the probability of success is the same and the trials are independent. The following table summarizes the four distributions related to drawing items:
| With replacements | No replacements | |
|---|---|---|
| Constant number of draws | binomial distribution | hypergeometric distribution |
| Constant number of failures | negative binomial distribution | negative hypergeometric distribution |
References
- 1 2 Negative hypergeometric distribution in Encyclopedia of Math.
| ||||||||||||||
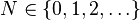 - total number of elements
- total number of elements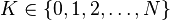 - total number of 'success' elements
- total number of 'success' elements