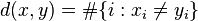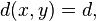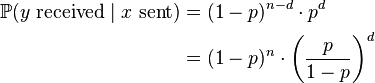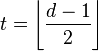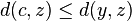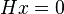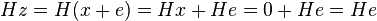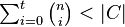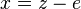Decoding methods
In coding theory, decoding is the process of translating received messages into codewords of a given code. There have been many common methods of mapping messages to codewords. These are often used to recover messages sent over a noisy channel, such as a binary symmetric channel.
Notation
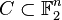 is considered a binary code with the length
is considered a binary code with the length  ;
;  shall be elements of
shall be elements of 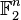 ; and
; and  is the distance between those elements.
is the distance between those elements.
Ideal observer decoding
One may be given the message 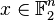 , then ideal observer decoding generates the codeword
, then ideal observer decoding generates the codeword 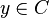 . The process results in this solution:
. The process results in this solution:
For example, a person can choose the codeword 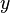 that is most likely to be received as the message
that is most likely to be received as the message  after transmission.
after transmission.
Decoding conventions
Each codeword does not have an expected possibility: there may be more than one codeword with an equal likelihood of mutating into the received message. In such a case, the sender and receiver(s) must agree ahead of time on a decoding convention. Popular conventions include:
- Request that the codeword be resent -- automatic repeat-request
- Choose any random codeword from the set of most likely codewords which is nearer to that.
Maximum likelihood decoding
Given a received codeword 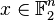 maximum likelihood decoding picks a codeword
maximum likelihood decoding picks a codeword 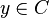 that maximizes
that maximizes
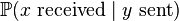 ,
,
that is, the codeword 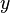 that maximizes the probability that
that maximizes the probability that  was received, given that
was received, given that 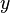 was sent. If all codewords are equally likely to be sent then this scheme is equivalent to ideal observer decoding.
In fact, by Bayes Theorem,
was sent. If all codewords are equally likely to be sent then this scheme is equivalent to ideal observer decoding.
In fact, by Bayes Theorem,
Upon fixing 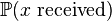 ,
,  is restructured and
is restructured and
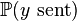 is constant as all codewords are equally likely to be sent.
Therefore
is constant as all codewords are equally likely to be sent.
Therefore
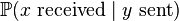 is maximised as a function of the variable
is maximised as a function of the variable 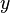 precisely when
precisely when
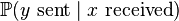 is maximised, and the claim follows.
is maximised, and the claim follows.
As with ideal observer decoding, a convention must be agreed to for non-unique decoding.
The maximum likelihood decoding problem can also be modeled as an integer programming problem.[1]
The maximum likelihood decoding algorithm is an instance of the "marginalize a product function" problem which is solved by applying the generalized distributive law.[2]
Minimum distance decoding
Given a received codeword 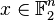 , minimum distance decoding picks a codeword
, minimum distance decoding picks a codeword 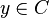 to minimise the Hamming distance :
to minimise the Hamming distance :
i.e. choose the codeword 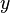 that is as close as possible to
that is as close as possible to  .
.
Note that if the probability of error on a discrete memoryless channel  is strictly less than one half, then minimum distance decoding is equivalent to maximum likelihood decoding, since if
is strictly less than one half, then minimum distance decoding is equivalent to maximum likelihood decoding, since if
then:
which (since p is less than one half) is maximised by minimising d.
Minimum distance decoding is also known as nearest neighbour decoding. It can be assisted or automated by using a standard array. Minimum distance decoding is a reasonable decoding method when the following conditions are met:
- The probability
 that an error occurs is independent of the position of the symbol
that an error occurs is independent of the position of the symbol - Errors are independent events - an error at one position in the message does not affect other positions
- The probability
These assumptions may be reasonable for transmissions over a binary symmetric channel. They may be unreasonable for other media, such as a DVD, where a single scratch on the disk can cause an error in many neighbouring symbols or codewords.
As with other decoding methods, a convention must be agreed to for non-unique decoding.
Syndrome decoding
Syndrome decoding is a highly efficient method of decoding a linear code over a noisy channel - i.e. one on which errors are made. In essence, syndrome decoding is minimum distance decoding using a reduced lookup table. This is allowed by the linearity of the code.
Suppose that 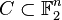 is a linear code of length
is a linear code of length  and minimum distance
and minimum distance 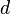 with parity-check matrix
with parity-check matrix  . Then clearly
. Then clearly 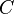 is capable of correcting up to
is capable of correcting up to
errors made by the channel (since if no more than  errors are made then minimum distance decoding will still correctly decode the incorrectly transmitted codeword).
errors are made then minimum distance decoding will still correctly decode the incorrectly transmitted codeword).
Now suppose that a codeword 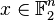 is sent over the channel and the error pattern
is sent over the channel and the error pattern 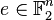 occurs. Then
occurs. Then 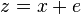 is received. Ordinary minimum distance decoding would lookup the vector
is received. Ordinary minimum distance decoding would lookup the vector 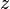 in a table of size
in a table of size 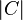 for the nearest match - i.e. an element (not necessarily unique)
for the nearest match - i.e. an element (not necessarily unique) 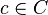 with
with
for all 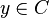 . Syndrome decoding takes advantage of the property of the parity matrix that:
. Syndrome decoding takes advantage of the property of the parity matrix that:
for all 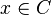 . The syndrome of the received
. The syndrome of the received 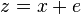 is defined to be:
is defined to be:
Under the assumption that no more than  errors were made during transmission, the receiver looks up the value
errors were made during transmission, the receiver looks up the value 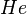 in a table of size
in a table of size
(for a binary code) against pre-computed values of 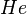 for all possible error patterns
for all possible error patterns 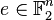 . Knowing what
. Knowing what  is, it is then trivial to decode
is, it is then trivial to decode  as:
as:
Partial response maximum likelihood
Partial response maximum likelihood (PRML) is a method for converting the weak analog signal from the head of a magnetic disk or tape drive into a digital signal.
Viterbi decoder
A Viterbi decoder uses the Viterbi algorithm for decoding a bitstream that has been encoded using forward error correction based on a convolutional code. The Hamming distance is used as a metric for hard decision Viterbi decoders. The squared Euclidean distance is used as a metric for soft decision decoders.
See also
Sources
- Hill, Raymond (1986). A first course in coding theory. Oxford Applied Mathematics and Computing Science Series. Oxford University Press. ISBN 0-19-853803-0.
- Pless, Vera (1982). Introduction to the theory of error-correcting codes. Wiley-Interscience Series in Discrete Mathematics. John Wiley & Sons. ISBN 0-471-08684-3.
- J.H. van Lint (1992). Introduction to Coding Theory. GTM 86 (2nd ed.). Springer-Verlag. ISBN 3-540-54894-7.
References
- ↑ Feldman, Jon; Wainwright, Martin J.; Karger, David R. (March 2005). "Using Linear Programming to Decode Binary Linear Codes". IEEE Transactions on Information Theory 51 (3). pp. 954–972. doi:10.1109/TIT.2004.842696.
- ↑ Aji, Srinivas M.; McEliece, Robert J. (March 2000). "The Generalized Distributive Law". IEEE Transactions on Information Theory 46 (2): 325–343. doi:10.1109/18.825794.