Natural neighbor

Natural neighbor interpolation. The area of the green circles are the interpolating weights, wi. The purple-shaded region is the new Voronoi cell, after inserting the point to be interpolated (black dot). The weights represent the intersection areas of the purple-cell with each of the 7 surrounding cells.
Natural neighbor interpolation is a method of spatial interpolation, developed by Robin Sibson.[1] The method is based on Voronoi tessellation of a discrete set of spatial points. This has advantages over simpler methods of interpolation, such as nearest-neighbor interpolation, in that it provides a smoother approximation to the underlying "true" function.
The basic equation in 2D is:
where 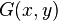 is the estimate at
is the estimate at 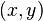 ,
,  are the weights and
are the weights and  are the known data at
are the known data at  . The weights,
. The weights,  , are calculated by finding how much of each of the surrounding areas is "stolen" when inserting
, are calculated by finding how much of each of the surrounding areas is "stolen" when inserting 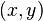 into the tessellation.
into the tessellation.
See also
References
- ↑ Sibson, R. (1981). "A brief description of natural neighbor interpolation (Chapter 2)". In V. Barnett. Interpreting Multivariate Data. Chichester: John Wiley. pp. 21–36.
External links
- Natural Neighbor Interpolation
- Implementation notes for natural neighbor, and comparison to other interpolation methods
- Interactive Voronoi diagram and natural neighbor interpolation visualization
This article is issued from Wikipedia - version of the Tuesday, March 31, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
