Bargaining problem

The two-person bargaining problem is a problem of understanding how two agents should cooperate when non-cooperation leads to Pareto-inefficient results. It is in essence an equilibrium selection problem; many games have multiple equilibria with varying payoffs for each player, forcing the players to negotiate on which equilibrium to target. Solutions to bargaining come in two flavors: an axiomatic approach where desired properties of a solution are satisfied and a strategic approach where the bargaining procedure is modeled in detail as a sequential game.

The bargaining game

The bargaining game or Nash bargaining game is a simple two-player game used to model bargaining interactions. In the Nash bargaining game, two players demand a portion of some good (usually some amount of money). If the total amount requested by the players is less than that available, both players get their request. If their total request is greater than that available, neither player gets their request. A Nash bargaining solution is a Pareto efficient solution to a Nash bargaining game. According to Walker,^[1] Nash's bargaining solution was shown by John Harsanyi to be the same as Zeuthen's solution^[2] of the bargaining problem.

Formal description

A two-person bargain problem consists of:

A feasibility set $F$ , a closed convex subset of 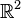$\mathbb{R}^2$ , the elements of which are interpreted as agreements. Set $F$ is convex because an agreement could take the form of a correlated combination of other agreements.
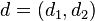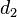A disagreement, or threat, point $d=(d_1, d_2)$ , where $d_1$ and $d_2$ are the respective payoffs to player 1 and player 2.

The problem is nontrivial if agreements in $F$ are better for both parties than the disagreement. The goal of bargaining is to choose the feasible agreement $\phi$ in $F$ that could result from negotiations.

Feasibility set

Which agreements are feasible depends on whether bargaining is mediated by an additional party:

When binding contracts are allowed, any joint action is playable, and the feasibility set consists of all attainable payoffs better than the disagreement point.
When binding contracts are unavailable, the players can defect (moral hazard), and the feasibility set is composed of correlated equilibria, since these outcomes require no exogenous enforcement.

Disagreement point

The disagreement point 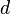$d$ is the value the players can expect to receive if negotiations break down. This could be some focal equilibrium that both players could expect to play. This point directly affects the bargaining solution, however, so it stands to reason that each player should attempt to choose his disagreement point in order to maximize his bargaining position. Towards this objective, it is often advantageous to increase one's own disagreement payoff while harming the opponent's disagreement payoff (hence the interpretation of the disagreement as a threat). If threats are viewed as actions, then one can construct a separate game wherein each player chooses a threat and receives a payoff according to the outcome of bargaining. It is known as Nash's variable threat game. Alternatively, each player could play a minimax strategy in case of disagreement, choosing to disregard personal reward in order to hurt the opponent as much as possible should the opponent leave the bargaining table.

Equilibrium analysis

Strategies are represented in the Nash bargaining game by a pair (x, y). x and y are selected from the interval [d, z], where d is the disagreement point and z is the total amount of good. If x + y is equal to or less than z, the first player receives x and the second y. Otherwise both get d; often $d=0$ .

There are many Nash equilibria in the Nash bargaining game. Any x and y such that x + y = z is a Nash equilibrium. If either player increases their demand, both players receive nothing. If either reduces their demand they will receive less than if they had demanded x or y. There is also a Nash equilibrium where both players demand the entire good. Here both players receive nothing, but neither player can increase their return by unilaterally changing their strategy.

Bargaining solutions

Various solutions have been proposed based on slightly different assumptions about what properties are desired for the final agreement point.

Nash bargaining solution

John Nash proposed^[3] that a solution should satisfy certain axioms:

Invariant to affine transformations or Invariant to equivalent utility representations
Pareto optimality
Independence of irrelevant alternatives
Symmetry

Nash proved that the solutions satisfying these axioms are exactly the points 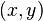$(x,y)$ which maximize the following expression:

(u(x)-u(d))(v(y)-v(d))

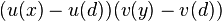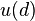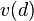where u and v are the utility functions of Player 1 and Player 2, respectively. That is, players act as if they seek to maximize $(u(x)-u(d))(v(y)-v(d))$ , where $u(d)$ and $v(d)$ , are the status quo utilities (the utility obtained if one decides not to bargain with the other player). The product of the two excess utilities is generally referred to as the Nash product. Intuitively, the solution consists of each player getting her status quo payoff (i.e., noncooperative payoff) in addition to an equal share of the benefits occurring from cooperation.^[4]^:15–16

The Nash bargaining solution can be explained as the result of the following bargaining process:^[5]^:301-302

A current agreement, say 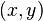$(x,y)$ , is on the table.
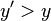One of the players, say player 2 can raise an objection. An objection is an alternative agreement, $(x',y')$ . Probably, the alternative agreement is better for player 2 ( $y'>y$ ) and worse for player 1 ( 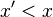$x'<x$ ). Raising such an objection has some probability of ending the negotiation. This probability, $p$ , can be selected by player 2 (e.g, by the amount of pressure he puts on player 1 to agree). 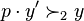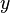The objection is effective only if $p\cdot y' \succ_2 y$ , i.e, player 2 prefers the alternative agreement $y'$ with a chance $p$ , over the original agreement $y$ for sure.
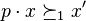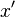Player 1 can then raise a counter-objection by claiming that for him, $p\cdot x \succeq_1 x'$ . This means that player 1 prefers to insist on the original agreement even if this might blow up the negotiation; player 1 prefers the original agreement $x$ with a chance $p$ , over the alternative agreement $x'$ for sure.
An agreement 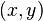$(x,y)$ is a Nash-bargaining-solution if, for every objection raised by one of the players, there is a counter-objection by the other player. It is an agreement which is robust to objections.

Kalai–Smorodinsky bargaining solution

Independence of Irrelevant Alternatives can be substituted with a monotonicity condition, as demonstrated by Ehud Kalai and Meir Smorodinsky.^[6] It is the point which maintains the ratios of maximal gains. 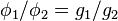In other words, if player 1 could receive a maximum of $g_1$ with player 2’s help (and vice versa for $g_2$ ), then the Kalai–Smorodinsky bargaining solution would yield the point $\phi$ on the Pareto frontier such that $\phi_1 / \phi_2 = g_1 / g_2$ .

Egalitarian bargaining solution

The egalitarian bargaining solution, introduced by Ehud Kalai,^[7] is a third solution which drops the condition of scale invariance while including both the axiom of Independence of irrelevant alternatives, and the axiom of monotonicity. It is the solution which attempts to grant equal gain to both parties. In other words, it is the point which maximizes the minimum payoff among players. Kalai notes that this solution is closely related to the ideas of John Rawls.

Comparison table

Name	Pareto-optimality	Symmetry	Scale-invariance	Irrelevant-independence	Monotonicity	Principle
Nash (1950)						Maximizing the product of surplus utilities
Kalai-Smorodinsky (1975)						Equalizing the ratios of maximal gains
Kalai (1977)						Maximizing the minimum of surplus utilities

Applications

Some philosophers and economists have recently used the Nash bargaining game to explain the emergence of human attitudes toward distributive justice.^[8]^[9]^[10]^[11] These authors primarily use evolutionary game theory to explain how individuals come to believe that proposing a 50–50 split is the only just solution to the Nash bargaining game.

Bargaining solutions and risk-aversion

Some economists have studied the effects of risk aversion on the bargaining solution. Compare two similar bargaining problems A and B, where the feasible space and the utility of player 1 remain fixed, but the utility of player 2 is different: player 2 is more risk-averse in A than in B. Then, the payoff of player 2 in the Nash bargaining solution is smaller in A than in B.^[5]^:303-304 However, this is true only if the outcome itself is certain; if the outcome is risky, then a risk-averse player may get a better deal.^[12]

References

↑ Walker, Paul (2005). "History of Game Theory".
↑ Zeuthen, Frederik (1930). Problems of Monopoly and Economic Warfare.
↑ Nash, John (1950). "The Bargaining Problem". Econometrica 18 (2): 155–162. doi:10.2307/1907266. JSTOR 1907266.
↑ Muthoo, Abhinay (1999). Bargaining theory with applications. Cambridge University Press.
1 2 Osborne, Martin (1994). A Course in Game Theory. MIT Press. ISBN 0-262-15041-7.
↑ Kalai, Ehud & Smorodinsky, Meir (1975). "Other solutions to Nash’s bargaining problem". Econometrica 43 (3): 513–518. doi:10.2307/1914280. JSTOR 1914280.
↑ Kalai, Ehud (1977). "Proportional solutions to bargaining situations: Intertemporal utility comparisons". Econometrica 45 (7): 1623–1630. doi:10.2307/1913954. JSTOR 1913954.
↑ Alexander, Jason McKenzie (2000). "Evolutionary Explanations of Distributive Justice". Philosophy of Science 67 (3): 490–516. doi:10.1086/392792. JSTOR 188629.
↑ Alexander, Jason; Skyrms, Brian (1999). "Bargaining with Neighbors: Is Justice Contagious". Journal of Philosophy 96 (11): 588–598. doi:10.2307/2564625. JSTOR 2564625.
↑ Binmore, Kenneth (1998). Game Theory and the Social Contract Volume 2: Just Playing. Cambridge: MIT Press. ISBN 0-262-02444-6.
↑ Binmore, Kenneth (2005). Natural Justice. New York: Oxford University Press. ISBN 0-19-517811-4.
↑ Roth, Alvin E.; Rothblum, Uriel G. (1982). "Risk Aversion and Nash's Solution for Bargaining Games with Risky Outcomes". Econometrica 50 (3): 639. doi:10.2307/1912605. JSTOR 1912605.

Binmore, K.; Rubinstein, A.; Wolinsky, A. (1986). "The Nash Bargaining Solution in Economic Modelling". RAND Journal of Economics 17: 176–188. doi:10.2307/2555382. JSTOR 2555382.

External links

Nash bargaining solutions

Topics in game theory

Definitions	Normal-form game Extensive-form game Escalation of commitment Graphical game Cooperative game Succinct game Information set Hierarchy of beliefs Preference

Equilibrium concepts	Nash equilibrium Subgame perfection Mertens-stable equilibrium Bayesian-Nash Perfect Bayesian Trembling hand Proper equilibrium Epsilon-equilibrium Correlated equilibrium Sequential equilibrium Quasi-perfect equilibrium Evolutionarily stable strategy Risk dominance Core Shapley value Pareto efficiency Quantal response equilibrium Self-confirming equilibrium Strong Nash equilibrium Markov perfect equilibrium

Strategies	Dominant strategies Pure strategy Mixed strategy Tit for tat Grim trigger Collusion Backward induction Forward induction Markov strategy

Classes of games	Symmetric game Perfect information Simultaneous game Sequential game Repeated game Signaling game Cheap talk Zero-sum game Mechanism design Bargaining problem Stochastic game n-player game Large Poisson game Nontransitive game Global games Strictly determined game

Games	Prisoner's dilemma Traveler's dilemma Coordination game Chicken Centipede game Volunteer's dilemma Dollar auction Battle of the sexes Stag hunt Matching pennies Ultimatum game Rock-paper-scissors Pirate game Dictator game Public goods game Blotto games War of attrition El Farol Bar problem Fair division Fair cake-cutting Cournot game Deadlock Diner's dilemma Guess 2/3 of the average Kuhn poker Nash bargaining game Screening game Prisoners and hats puzzle Trust game Princess and monster game Monty Hall problem Rendezvous problem

Theorems	Minimax theorem Nash's theorem Purification theorem Folk theorem Revelation principle Arrow's impossibility theorem

Key figures	Kenneth Arrow Robert Aumann Kenneth Binmore Samuel Bowles Melvin Dresher Merrill M. Flood Drew Fudenberg Donald B. Gillies John Harsanyi Leonid Hurwicz David K. Levine Daniel Kahneman David M. Kreps Harold W. Kuhn Eric Maskin Jean-François Mertens Paul Milgrom Oskar Morgenstern Hervé Moulin Roger Myerson John Nash John von Neumann Ariel Rubinstein Thomas Schelling Reinhard Selten Herbert Simon Lloyd Shapley John Maynard Smith Jean Tirole Albert W. Tucker Amos Tversky William Vickrey Robert B. Wilson Peyton Young

See also	Tragedy of the commons Tyranny of small decisions All-pay auction List of games in game theory Confrontation analysis List of game theorists Combinatorial game theory Alpha–beta pruning Bertrand paradox Bounded rationality No-win situation Coopetition

This article is issued from Wikipedia - version of the Wednesday, January 27, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.