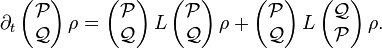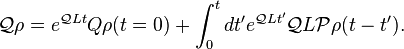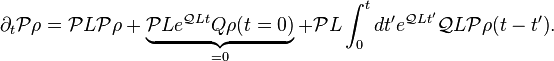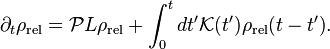Nakajima–Zwanzig equation
The Nakajima–Zwanzig equation (named after the physicists Sadao Nakajima and Robert Zwanzig) is an integral equation describing the time evolution of the "relevant" part of a quantum-mechanical system. It is formulated in the density matrix formalism and can be regarded a generalization of the Master equation.
The equation belongs to the Mori–Zwanzig theory within the statistical mechanics of irreversible processes (named after Hazime Mori). By means of a projection operator the dynamics is split into a slow, collective part (relevant part) and a rapidly fluctuating irrelevant part. The goal is to develop dynamical equations for the collective part.
Derivation
The starting point[1] is the quantum mechanical Liouville equation (von Neumann equation)
where the Liouville operator  is defined as
is defined as ![L A = \frac{i}{\hbar}[A,H]](../I/m/0a2b6dfc97a0a90b48dc0ea123c50118.png) .
.
The density operator (density matrix)  is split by means of a projection operator
is split by means of a projection operator
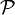 into two parts
into two parts
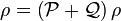 ,
where
,
where 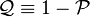 . The projection operator
. The projection operator 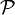 projects onto the aforementioned relevant part, for which an equation of motion is to be derived.
projects onto the aforementioned relevant part, for which an equation of motion is to be derived.
The Liouville – von Neumann equation can thus be represented as
The second line is formally solved as[2]
By plugging the solution into the first equation, we obtain the Nakajima–Zwanzig equation:
Under the assumption that the inhomogeneous term vanishes[3] and using
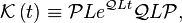
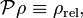 as well as
as well as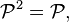
we obtain the final form
References
- E. Fick, G. Sauermann: The Quantum Statistics of Dynamic Processes Springer-Verlag, 1983, ISBN ISSN 3-540-50824-4.
- Heinz-Peter Breuer, Francesco Petruccione: Theory of Open Quantum Systems. Oxford, 2002 ISBN ISSN 970-0-19-852063-4
- Hermann Grabert Projection operator techniques in nonequilibrium statistical mechanics, Springer Tracts in Modern Physics, Band 95, 1982
- R. Kühne, P. Reineker: Nakajima-Zwanzig's generalized master equation: Evaluation of the kernel of the integro-differential equation, Zeitschrift für Physik B (Condensed Matter), Band 31, 1978, S. 105–110, Abstract
Original works
- Sadao Nakajima (1958), "On Quantum Theory of Transport Phenomena" (in German), Progress of Theoretical Physics 20 (6): pp. 948–959
- Robert Zwanzig (1960), "Ensemble Method in the Theory of Irreversibility" (in German), Journal of Chemical Physics 33 (5): pp. 1338–1341
- original paper
Notes
- ↑ A derivation analogous to that presented here is found, for instance, in Breuer, Petruccione The theory of open quantum systems, Oxford University Press 2002, S.443ff
- ↑ To verify the equation it suffices to write the function under the integral as a derivative, deQLt'QeL(t-t') = -eQLt'QLPeL(t-t')dt'.
- ↑ Such an assumption can be made if we assume that the irrelevant part of the density matrix is 0 at the initial time, so that the projector for t=0 is the identity.
![\partial_t \rho = \frac{i}{\hbar}[\rho,H] = L \rho,](../I/m/7d0a056c356645f6b82b863e3a886075.png)