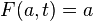Retract
In topology, a branch of mathematics, a retraction[1] is a continuous mapping from the entire space into a subspace which preserves the position of all points in that subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.
Definitions
Retract
Let X be a topological space and A a subspace of X. Then a continuous map
is a retraction if the restriction of r to A is the identity map on A; that is, r(a) = a for all a in A. Equivalently, denoting by
the inclusion, a retraction is a continuous map r such that
that is, the composition of r with the inclusion is the identity of A. Note that, by definition, a retraction maps X onto A. A subspace A is called a retract of X if such a retraction exists. For instance, any non-empty space retracts to a point in the obvious way (the constant map yields a retraction). If X is Hausdorff, then A must be closed.
If 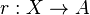 is a retraction, then the composition
is a retraction, then the composition 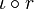 is an idempotent continuous map from X to X. Conversely, given any idempotent continuous map
is an idempotent continuous map from X to X. Conversely, given any idempotent continuous map  , we obtain a retraction onto the image of s by restricting the codomain.
, we obtain a retraction onto the image of s by restricting the codomain.
A space X is known as an absolute retract if for every normal space Y that contains X as a closed subspace, X is a retract of Y. The unit cube In as well as the Hilbert cube Iω are absolute retracts.
Neighborhood retract
If there exists an open set U such that
and A is a retract of U, then A is called a neighborhood retract of X.
A space X is an absolute neighborhood retract (or ANR) if for every normal space Y that embeds X as a closed subset, X is a neighborhood retract of Y. The n-sphere Sn is an absolute neighborhood retract.
Deformation retract and strong deformation retract
A continuous map
is a deformation retraction of a space X onto a subspace A if, for every x in X and a in A,
In other words, a deformation retraction is a homotopy between a retraction and the identity map on X. The subspace A is called a deformation retract of X. A deformation retraction is a special case of homotopy equivalence.
A retract need not be a deformation retract. For instance, having a single point as a deformation retract would imply a space is path connected (in fact, it would imply contractibility of the space).
Note: An equivalent definition of deformation retraction is the following. A continuous map r: X → A is a deformation retraction if it is a retraction and its composition with the inclusion is homotopic to the identity map on X. In this formulation, a deformation retraction carries with it a homotopy between the identity map on X and itself.
If, in the definition of a deformation retraction, we add the requirement that
for all t in [0, 1] and a in A, then F is called a strong deformation retraction. In other words, a strong deformation retraction leaves points in A fixed throughout the homotopy. (Some authors, such as Allen Hatcher, take this as the definition of deformation retraction.)
As an example, the n-sphere Sn is a strong deformation retract of Rn+1\{0}; as strong deformation retraction one can choose the map
Neighborhood deformation retract
A closed subspace A is a neighborhood deformation retract of X if there exists a continuous map  (where
(where ![I=[0,1]](../I/m/e56ebb3d9782176e00be7a6f25e2f8df.png) ) such that
) such that 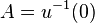 and a homotopy
and a homotopy
 such that
such that  for all
for all  ,
,  for all
for all
 , and
, and  for all
for all  .[2]
.[2]
Properties
- The main obvious property of a retract A of X is that any continuous map
 has at least one extension
has at least one extension  , namely,
, namely,  .
.
- Deformation retraction is a particular case of homotopy equivalence. In fact, two spaces are homotopy equivalent if and only if they are both deformation retracts of a single larger space.
- Any topological space which deformation retracts to a point is contractible and vice versa. However, there exist contractible spaces which do not strongly deformation retract to a point.[3]
No-retraction theorem
The boundary of the n-dimensional ball, that is, the (n − 1)-sphere, is not a retract of the ball, which is known as the no-retraction theorem. (See Brouwer fixed-point theorem#A proof using homology.)
Notes
- ↑ K. Borsuk (1931). "Sur les rétractes". Fund. Math. 17: 2–20.
- ↑ Steenrod, N. E. (1967). "A convenient category of topological spaces". Michigan Math. J. 14 (2): 133–152. doi:10.1307/mmj/1028999711.
- ↑ Hatcher, Allen (2002), Algebraic topology, Cambridge University Press, ISBN 978-0-521-79540-1
References
- J.P. May, A concise course in algebraic topology
- Munkres, James; Topology, Prentice Hall; 2nd edition (December 28, 1999). ISBN 0-13-181629-2.
External links
- This article incorporates material from Neighborhood retract on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.



![F:X \times [0, 1] \to X \,](../I/m/e8160f3e767503fd2d836a2c86d0a8a2.png)