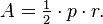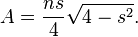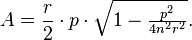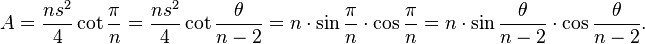Polygon

In elementary geometry, a polygon /ˈpɒlɪɡɒn/ is a plane figure that is bounded by a finite chain of straight line segments closing in a loop to form a closed chain or circuit. These segments are called its edges or sides, and the points where two edges meet are the polygon's vertices (singular: vertex) or corners. The interior of the polygon is sometimes called its body. An n-gon is a polygon with n sides. A polygon is a 2-dimensional example of the more general polytope in any number of dimensions.
The basic geometrical notion of a polygon has been adapted in various ways to suit particular purposes. Mathematicians are often concerned only with the bounding closed polygonal chain and with simple polygons which do not self-intersect, and they often define a polygon accordingly. A polygonal boundary may be allowed to intersect itself, creating star polygons. Geometrically two edges meeting at a corner are required to form an angle that is not straight (180°); otherwise, the line segments may be considered parts of a single edge; however mathematically, such corners may sometimes be allowed. These and other generalizations of polygons are described below.
Etymology
The word "polygon" derives from the Greek πολύς (polús) "much", "many" and γωνία (gōnía) "corner" or "angle". It has been suggested that γόνυ (gónu) "knee" may be the origin of “gon”,[1]
Classification
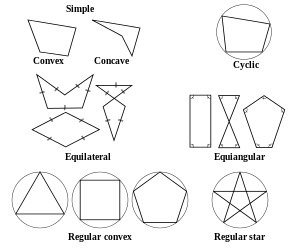
Number of sides
Polygons are primarily classified by the number of sides. See table below.
Convexity and non-convexity
Polygons may be characterized by their convexity or type of non-convexity:
- Convex: any line drawn through the polygon (and not tangent to an edge or corner) meets its boundary exactly twice. As a consequence, all its interior angles are less than 180°. Equivalently, any line segment with endpoints on the boundary passes through only interior points between its endpoints.
- Non-convex: a line may be found which meets its boundary more than twice. Equivalently, there exists a line segment between two boundary points that passes outside the polygon.
- Simple: the boundary of the polygon does not cross itself. All convex polygons are simple.
- Concave: Non-convex and simple. There is at least one interior angle greater than 180°.
- Star-shaped: the whole interior is visible from a single point, without crossing any edge. The polygon must be simple, and may be convex or concave.
- Self-intersecting: the boundary of the polygon crosses itself. Branko Grünbaum calls these coptic, though this term does not seem to be widely used. The term complex is sometimes used in contrast to simple, but this usage risks confusion with the idea of a complex polygon as one which exists in the complex Hilbert plane consisting of two complex dimensions.
- Star polygon: a polygon which self-intersects in a regular way. A polygon cannot be both a star and star-shaped.
Equality and symmetry
- Equiangular: all corner angles are equal.
- Cyclic: all corners lie on a single circle, called the circumcircle.
- Isogonal or vertex-transitive: all corners lie within the same symmetry orbit. The polygon is also cyclic and equiangular.
- Equilateral: all edges are of the same length. The polygon need not be convex.
- Tangential: all sides are tangent to an inscribed circle.
- Isotoxal or edge-transitive: all sides lie within the same symmetry orbit. The polygon is also equilateral and tangential.
- Regular: the polygon is both isogonal and isotoxal. Equivalently, it is both cyclic and equilateral, or both equilateral and equiangular. A non-convex regular polygon is called a regular star polygon.
Miscellaneous
- Rectilinear: the polygon's sides meet at right angles, i.e., all its interior angles are 90 or 270 degrees.
- Monotone with respect to a given line L: every line orthogonal to L intersects the polygon not more than twice.
Properties and Formulas
Euclidean geometry is assumed throughout.
Angles
Any polygon has as many corners as it has sides. Each corner has several angles. The two most important ones are:
- Interior angle – The sum of the interior angles of a simple n-gon is (n − 2)π radians or (n − 2) × 180 degrees. This is because any simple n-gon ( having " n" sides ) can be considered to be made up of (n − 2) triangles, each of which has an angle sum of π radians or 180 degrees. The measure of any interior angle of a convex regular n-gon is
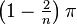 radians or
radians or 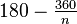 degrees. The interior angles of regular star polygons were first studied by Poinsot, in the same paper in which he describes the four regular star polyhedra: for a regular
degrees. The interior angles of regular star polygons were first studied by Poinsot, in the same paper in which he describes the four regular star polyhedra: for a regular 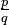 -gon (a p-gon with central density q), each interior angle is
-gon (a p-gon with central density q), each interior angle is 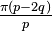 radians or
radians or 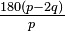 degrees.[2]
degrees.[2] - Exterior angle – The exterior angle is the supplementary angle to the interior angle. Tracing around a convex n-gon, the angle "turned" at a corner is the exterior or external angle. Tracing all the way around the polygon makes one full turn, so the sum of the exterior angles must be 360°. This argument can be generalized to concave simple polygons, if external angles that turn in the opposite direction are subtracted from the total turned. Tracing around an n-gon in general, the sum of the exterior angles (the total amount one rotates at the vertices) can be any integer multiple d of 360°, e.g. 720° for a pentagram and 0° for an angular "eight" or antiparallelogram, where d is the density or starriness of the polygon. See also orbit (dynamics).
Area and centroid
Simple polygons
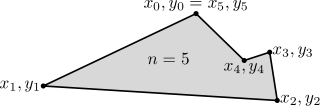
For a non-self-intersecting (simple) polygon with n vertices xi, yi ( i = 1 to n), the area and centroid are given by:[3]
To close the polygon, the first and last vertices are the same, i.e., xn, yn = x0, y0. The vertices must be ordered according to positive or negative orientation (counterclockwise or clockwise, respectively); if they are ordered negatively, the value given by the area formula will be negative but correct in absolute value, but when calculating 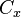 and
and  , the signed value of
, the signed value of  (which in this case is negative) should be used. This is commonly called the Shoelace formula or Surveyor's formula.[4]
(which in this case is negative) should be used. This is commonly called the Shoelace formula or Surveyor's formula.[4]
The area A of a simple polygon can also be computed if the lengths of the sides, a1, a2, ..., an and the exterior angles, θ1, θ2, ..., θn are known, from:
The formula was described by Lopshits in 1963.[5]
If the polygon can be drawn on an equally spaced grid such that all its vertices are grid points, Pick's theorem gives a simple formula for the polygon's area based on the numbers of interior and boundary grid points.
In every polygon with perimeter p and area A , the isoperimetric inequality 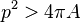 holds.[6]
holds.[6]
If any two simple polygons of equal area are given, then the first can be cut into polygonal pieces which can be reassembled to form the second polygon. This is the Bolyai–Gerwien theorem.
The area of a regular polygon is also given in terms of the radius r of its inscribed circle and its perimeter p by
This radius is also termed its apothem and is often represented as a.
The area of a regular n-gon with side s inscribed in a unit circle is
The area of a regular n-gon in terms of the radius r of its circumscribed circle and its perimeter p is given by
The area of a regular n-gon, inscribed in a unit-radius circle, with side s and interior angle θ can also be expressed trigonometrically as
The lengths of the sides of a polygon do not in general determine the area.[7] However, if the polygon is cyclic the sides do determine the area. Of all n-gons with given sides, the one with the largest area is cyclic. Of all n-gons with a given perimeter, the one with the largest area is regular (and therefore cyclic).[8]
Self-intersecting polygons
The area of a self-intersecting polygon can be defined in two different ways, each of which gives a different answer:
- Using the above methods for simple polygons, we allow that particular regions within the polygon may have their area multiplied by a factor which we call the density of the region. For example the central convex pentagon in the center of a pentagram has density 2. The two triangular regions of a cross-quadrilateral (like a figure 8) have opposite-signed densities, and adding their areas together can give a total area of zero for the whole figure.
- Considering the enclosed regions as point sets, we can find the area of the enclosed point set. This corresponds to the area of the plane covered by the polygon, or to the area of one or more simple polygons having the same outline as the self-intersecting one. In the case of the cross-quadrilateral, it is treated as two simple triangles.
Generalizations of polygons
The idea of a polygon has been generalized in various ways. Some of the more important include:
- A spherical polygon is a circuit of arcs of great circles (sides) and vertices on the surface of a sphere. It allows the digon, a polygon having only two sides and two corners, which is impossible in a flat plane. Spherical polygons play an important role in cartography (map making) and in Wythoff's construction of the uniform polyhedra.
- A skew polygon does not lie in a flat plane, but zigzags in three (or more) dimensions. The Petrie polygons of the regular polytopes are well known examples.
- An apeirogon is an infinite sequence of sides and angles, which is not closed but has no ends because it extends indefinitely in both directions.
- A skew apeirogon is an infinite sequence of sides and angles that do not lie in a flat plane.
- A complex polygon is a configuration analogous to an ordinary polygon, which exists in the complex plane of two real and two imaginary dimensions.
- An abstract polygon is an algebraic partially ordered set representing the various elements (sides, vertices, etc.) and their connectivity. A real geometric polygon is said to be a realization of the associated abstract polygon. Depending on the mapping, all the generalizations described here can be realized.
- A polyhedron is a three-dimensional solid bounded by flat polygonal faces, analogous to a polygon in two dimensions. The corresponding shapes in four or higher dimensions are called polytopes.
Naming polygons
The word "polygon" comes from Late Latin polygōnum (a noun), from Greek πολύγωνον (polygōnon/polugōnon), noun use of neuter of πολύγωνος (polygōnos/polugōnos, the masculine adjective), meaning "many-angled". Individual polygons are named (and sometimes classified) according to the number of sides, combining a Greek-derived numerical prefix with the suffix -gon, e.g. pentagon, dodecagon. The triangle, quadrilateral and nonagon are exceptions.
Beyond decagons (10-sided) and dodecagons (12-sided), mathematicians generally use numerical notation, for example 17-gon and 257-gon.[9]
Exceptions exist for side counts that are more easily expressed in verbal form (e.g. 20 and 30), or are used by non-mathematicians. Some special polygons also have their own names; for example the regular star pentagon is also known as the pentagram.
| Name | Edges | Properties |
|---|---|---|
| monogon | 1 | Not generally recognised as a polygon,[10] although some disciplines such as graph theory sometimes use the term.[11] |
| digon | 2 | Not generally recognised as a polygon in the Euclidean plane, although it can exist as a spherical polygon.[12] |
| triangle (or trigon) | 3 | The simplest polygon which can exist in the Euclidean plane. Can tile the plane. |
| quadrilateral (or tetragon) | 4 | The simplest polygon which can cross itself; the simplest polygon which can be concave; the simplest polygon which can be non-cyclic. Can tile the plane. |
| pentagon | 5 | [13] The simplest polygon which can exist as a regular star. A star pentagon is known as a pentagram or pentacle. |
| hexagon | 6 | [13] Can tile the plane. |
| heptagon | 7 | [13] The simplest polygon such that the regular form is not constructible with compass and straightedge. However, it can be constructed using a Neusis construction. |
| octagon | 8 | [13] |
| nonagon (or enneagon) | 9 | [13]"Nonagon" mixes Latin [novem = 9] with Greek, "enneagon" is pure Greek. |
| decagon | 10 | [13] |
| hendecagon (or undecagon) | 11 | [13] The simplest polygon such that the regular form cannot be constructed with compass, straightedge, and angle trisector. |
| dodecagon (or duodecagon) | 12 | [13] |
| tridecagon (or triskaidecagon) | 13 | [13] |
| tetradecagon (or tetrakaidecagon) | 14 | [13] |
| pentadecagon (or pentakaidecagon) | 15 | [13] |
| hexadecagon (or hexakaidecagon) | 16 | [13] |
| heptadecagon (or heptakaidecagon) | 17 | Constructible polygon[9] |
| octadecagon (or octakaidecagon) | 18 | [13] |
| enneadecagon (or enneakaidecagon) | 19 | [13] |
| icosagon | 20 | [13] |
| icositetragon (or icosikaitetragon) | 24 | [13] |
| triacontagon | 30 | [13] |
| tetracontagon (or tessaracontagon) | 40 | [13][14] |
| pentacontagon (or pentecontagon) | 50 | [13][14] |
| hexacontagon (or hexecontagon) | 60 | [13][14] |
| heptacontagon (or hebdomecontagon) | 70 | [13][14] |
| octacontagon (or ogdoëcontagon) | 80 | [13][14] |
| enneacontagon (or enenecontagon) | 90 | [13][14] |
| hectogon (or hecatontagon)[15] | 100 | [13] |
| 257 | Constructible polygon[9] | |
| chiliagon | 1000 | Philosophers including René Descartes,[16] Immanuel Kant,[17] David Hume,[18] have used the chiliagon as an example in discussions. |
| myriagon | 10,000 | Used as an example in some philosophical discussions, for example in Descartes' Meditations on First Philosophy |
| 65,537 | Constructible polygon[9] | |
| megagon[19][20][21] | 1,000,000 | As with René Descartes' example of the chiliagon, the million-sided polygon has been used as an illustration of a well-defined concept that cannot be visualised.[22][23][24][25][26][27][28] The megagon is also used as an illustration of the convergence of regular polygons to a circle.[29] |
| apeirogon | ∞ | A degenerate polygon of infinitely many sides. |
Constructing higher names
To construct the name of a polygon with more than 20 and less than 100 edges, combine the prefixes as follows.[13] The "kai" term applies to 13-gons and higher was used by Kepler, and advocated by John H. Conway for clarity to concatenated prefix numbers in the naming of quasiregular polyhedra.[30]
| Tens | and | Ones | final suffix | ||
|---|---|---|---|---|---|
| -kai- | 1 | -hena- | -gon | ||
| 20 | icosi- (icosa- when alone) | 2 | -di- | ||
| 30 | triaconta- (or triconta-) | 3 | -tri- | ||
| 40 | tetraconta- (or tessaraconta-) | 4 | -tetra- | ||
| 50 | pentaconta- (or penteconta-) | 5 | -penta- | ||
| 60 | hexaconta- (or hexeconta-) | 6 | -hexa- | ||
| 70 | heptaconta- (or hebdomeconta-) | 7 | -hepta- | ||
| 80 | octaconta- (or ogdoëconta-) | 8 | -octa- | ||
| 90 | enneaconta- (or eneneconta-) | 9 | -ennea- | ||
History

Polygons have been known since ancient times. The regular polygons were known to the ancient Greeks, with the pentagram, a non-convex regular polygon (star polygon), appearing as early as the 7th century B.C. on a krater by Aristonothos, found at Caere and now in the Capitoline Museum.[31][32]
The first known systematic study of non-convex polygons in general was made by Thomas Bradwardine in the 14th century.[33]
In 1952, Geoffrey Colin Shephard generalized the idea of polygons to the complex plane, where each real dimension is accompanied by an imaginary one, to create complex polygons.[34]
Polygons in nature

Polygons appear in rock formations, most commonly as the flat facets of crystals, where the angles between the sides depend on the type of mineral from which the crystal is made.
Regular hexagons can occur when the cooling of lava forms areas of tightly packed columns of basalt, which may be seen at the Giant's Causeway in Northern Ireland, or at the Devil's Postpile in California.
In biology, the surface of the wax honeycomb made by bees is an array of hexagons, and the sides and base of each cell are also polygons.
Polygons in computer graphics
A polygon in a computer graphics (image generation) system is a two-dimensional shape that is modelled and stored within its database. A polygon can be colored, shaded and textured, and its position in the database is defined by the coordinates of its vertices (corners).
Naming conventions differ from those of mathematicians:
- A simple polygon does not cross itself.
- a concave polygon is a simple polygon having at least one interior angle greater than 180°.
- A complex polygon does cross itself.
Any surface is modelled as a tessellation called meshed polygons. If a square mesh has n + 1 points (vertices) per side, there are n squared squares in the mesh, or 2n squared triangles since there are two triangles in a square. There are (n + 1)2 / 2(n2) vertices per triangle. Where n is large, this approaches one half. Or, each vertex inside the square mesh connects four edges (lines).
The imaging system calls up the structure of polygons needed for the scene to be created from the database. This is transferred to active memory and finally, to the display system (screen, TV monitors etc.) so that the scene can be viewed. During this process, the imaging system renders polygons in correct perspective ready for transmission of the processed data to the display system. Although polygons are two-dimensional, through the system computer they are placed in a visual scene in the correct three-dimensional orientation.
In computer graphics and computational geometry, it is often necessary to determine whether a given point P = (x0,y0) lies inside a simple polygon given by a sequence of line segments. This is called the Point in polygon test.
See also
References
Bibliography
- Coxeter, H.S.M.; Regular Polytopes, (Methuen and Co., 1948).
- Cromwell, P.; Polyhedra, CUP hbk (1997), pbk. (1999).
- Grünbaum, B.; Are your polyhedra the same as my polyhedra? Discrete and comput. geom: the Goodman-Pollack festschrift, ed. Aronov et al. Springer (2003) pp. 461–488. (pdf)
Notes
- ↑ Craig, John (1849). A new universal etymological technological, and pronouncing dictionary of the English language. Oxford University. p. 404. Extract of page 404
- ↑ Kappraff, Jay (2002). Beyond measure: a guided tour through nature, myth, and number. World Scientific. p. 258. ISBN 978-981-02-4702-7.
- ↑ Bourke, Paul (July 1988). "Calculating The Area And Centroid Of A Polygon" (PDF). Retrieved 6 Feb 2013.
- ↑ Bart Braden (1986). "The Surveyor's Area Formula" (PDF). The College Mathematics Journal 17 (4): 326–337. doi:10.2307/2686282.
- ↑ A.M. Lopshits (1963). Computation of areas of oriented figures. translators: J Massalski and C Mills, Jr. D C Heath and Company: Boston, MA.
- ↑ Dergiades,Nikolaos, "An elementary proof of the isoperimetric inequality", Forum Mathematicorum 2, 2002, 129–130.
- ↑ Robbins, "Polygons inscribed in a circle," American Mathematical Monthly 102, June–July 1995.
- ↑ Chakerian, G. D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.
- 1 2 3 4 Mathworld
- ↑ Grunbaum, B.; "Are your polyhedra the same as my polyhedra", Discrete and computational geometry: the Goodman-Pollack Festschrift, Ed. Aronov et al., Springer (2003), page 464.
- ↑ Hass, Joel; Morgan, Frank (1996), "Geodesic nets on the 2-sphere", Proceedings of the American Mathematical Society 124 (12): 3843–3850, doi:10.1090/S0002-9939-96-03492-2, JSTOR 2161556, MR 1343696.
- ↑ Coxeter, H.S.M.; Regular polytopes, Dover Edition (1973), Page 4.
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Salomon, David (2011). The Computer Graphics Manual. Springer Science & Business Media. pp. 88–90. ISBN 978-0-85729-886-7.
- 1 2 3 4 5 6 The New Elements of Mathematics: Algebra and Geometry by Charles Sanders Peirce (1976), p.298
- ↑ http://mathforum.org/dr.math/faq/faq.polygon.names.html
- ↑ Sepkoski, David (2005). "Nominalism and constructivism in seventeenth-century mathematical philosophy" (PDF). Historia Mathematica 32: 33–59. doi:10.1016/j.hm.2003.09.002. Retrieved 18 April 2012.
- ↑ Gottfried Martin (1955), Kant's Metaphysics and Theory of Science, Manchester University Press, p. 22.
- ↑ David Hume, The Philosophical Works of David Hume, Volume 1, Black and Tait, 1826, p. 101.
- ↑ Gibilisco, Stan (2003). Geometry demystified (Online-Ausg. ed.). New York: McGraw-Hill. ISBN 978-0-07-141650-4.
- ↑ Darling, David J., The universal book of mathematics: from Abracadabra to Zeno's paradoxes, John Wiley & Sons, 2004. Page 249. ISBN 0-471-27047-4.
- ↑ Dugopolski, Mark, College Algebra and Trigonometry, 2nd ed, Addison-Wesley, 1999. Page 505. ISBN 0-201-34712-1.
- ↑ McCormick, John Francis, Scholastic Metaphysics, Loyola University Press, 1928, p. 18.
- ↑ Merrill, John Calhoun and Odell, S. Jack, Philosophy and Journalism, Longman, 1983, p. 47, ISBN 0-582-28157-1.
- ↑ Hospers, John, An Introduction to Philosophical Analysis, 4th ed, Routledge, 1997, p. 56, ISBN 0-415-15792-7.
- ↑ Mandik, Pete, Key Terms in Philosophy of Mind, Continuum International Publishing Group, 2010, p. 26, ISBN 1-84706-349-7.
- ↑ Kenny, Anthony, The Rise of Modern Philosophy, Oxford University Press, 2006, p. 124, ISBN 0-19-875277-6.
- ↑ Balmes, James, Fundamental Philosophy, Vol II, Sadlier and Co., Boston, 1856, p. 27.
- ↑ Potter, Vincent G., On Understanding Understanding: A Philosophy of Knowledge, 2nd ed, Fordham University Press, 1993, p. 86, ISBN 0-8232-1486-9.
- ↑ Russell, Bertrand, History of Western Philosophy, reprint edition, Routledge, 2004, p. 202, ISBN 0-415-32505-6.
- ↑ "Naming Polygons and Polyhedra". Ask Dr. Math. The Math Forum – Drexel University. Retrieved 3 May 2015.
- ↑ Heath, Sir Thomas Little (1981), A History of Greek Mathematics, Volume 1, Courier Dover Publications, p. 162, ISBN 9780486240732. Reprint of original 1921 publication with corrected errata. Heath uses the spelling "Aristonophus" for the vase painter's name.
- ↑ Cratere with the blinding of Polyphemus and a naval battle, Castellani Halls, Capitoline Museum, accessed 2013-11-11. Two pentagrams are visible near the center of the image,
- ↑ Coxeter, H.S.M.; Regular Polytopes, 3rd Edn, Dover (pbk), 1973, p.114
- ↑ Shephard, G.C.; "Regular complex polytopes", Proc. London Math. Soc. Series 3 Volume 2, 1952, pp 82-97
External links
| Look up polygon in Wiktionary, the free dictionary. |
| Wikimedia Commons has media related to Polygons. |
- Weisstein, Eric W., "Polygon", MathWorld.
- What Are Polyhedra?, with Greek Numerical Prefixes
- Polygons, types of polygons, and polygon properties, with interactive animation
- How to draw monochrome orthogonal polygons on screens, by Herbert Glarner
- comp.graphics.algorithms Frequently Asked Questions, solutions to mathematical problems computing 2D and 3D polygons
- Comparison of the different algorithms for Polygon Boolean operations, compares capabilities, speed and numerical robustness
- Interior angle sum of polygons: a general formula, Provides an interactive Java investigation that extends the interior angle sum formula for simple closed polygons to include crossed (complex) polygons
| ||||||||||||||||||||||||||
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
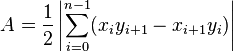
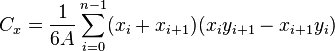
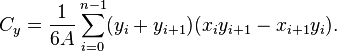
![\begin{align}A = \frac12 ( a_1[a_2 \sin(\theta_1) + a_3 \sin(\theta_1 + \theta_2) + \cdots + a_{n-1} \sin(\theta_1 + \theta_2 + \cdots + \theta_{n-2})] \\
{} + a_2[a_3 \sin(\theta_2) + a_4 \sin(\theta_2 + \theta_3) + \cdots + a_{n-1} \sin(\theta_2 + \cdots + \theta_{n-2})] \\
{} + \cdots + a_{n-2}[a_{n-1} \sin(\theta_{n-2})] ). \end{align}](../I/m/d0222575d13e2883862411ab82d64f17.png)