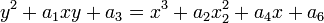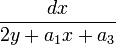Néron differential

In mathematics, a Néron differential, named after André Néron, is an almost canonical choice of 1-form on an elliptic curve or abelian variety defined over a local field or global field. The Néron differential behaves well on the Néron minimal models.

For an elliptic curve of the form

y^2+a_1xy+a_3=x^3+a_2x^2_2+a_4x+a_6

the Néron differential is

\frac{dx}{2y+a_1x+a_3}

References

Bosch, Siegfried; Lütkebohmert, Werner; Raynaud, Michel (1990), Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) 21, Berlin, New York: Springer-Verlag, ISBN 978-3-540-50587-7, MR 1045822
Néron, André (1964), "Modèles minimaux des variétes abèliennes sur les corps locaux et globaux", Publications Mathématiques de l'IHÉS 21: 5–128, doi:10.1007/BF02684271, MR 0179172

This article is issued from Wikipedia - version of the Thursday, September 25, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.