Multivalued dependency
In database theory, a multivalued dependency is a full constraint between two sets of attributes in a relation.
In contrast to the functional dependency, the multivalued dependency requires that certain tuples be present in a relation. Therefore, a multivalued dependency is a special case of tuple-generating dependency. The multivalued dependency plays a role in the 4NF database normalization.
A multivalued dependency is a special case of a join dependency, with only two sets of values involved, i.e. it is a 2-ary join dependency.
Formal definition
The formal definition is given as follows. [1]
Let
be a relational schema and let
and
(subsets). The multivalued dependency
(which can be read asmultidetermines
) holds on
if, in any legal relation
, for all pairs of tuples
and
in
such that
, there exist tuples
and
in
such that
In more simple words the above condition can be expressed as follows: if we denote by  the tuple having values for
the tuple having values for 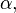

 collectively equal to
collectively equal to 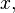
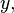
 correspondingly, then whenever the tuples
correspondingly, then whenever the tuples 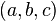 and
and  exist in
exist in  , the tuples
, the tuples 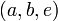 and
and 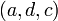 should also exist in
should also exist in  .
.
Example
Consider this example of a relation of university courses, the books recommended for the course, and the lecturers who will be teaching the course:
| Course | Book | Lecturer |
|---|---|---|
| AHA | Silberschatz | John D |
| AHA | Nederpelt | John D |
| AHA | Silberschatz | William M |
| AHA | Nederpelt | William M |
| AHA | Silberschatz | Christian G |
| AHA | Nederpelt | Christian G |
| OSO | Silberschatz | John D |
| OSO | Silberschatz | William M |
Because the lecturers attached to the course and the books attached to the course are independent of each other, this database design has a multivalued dependency; if we were to add a new book to the AHA course, we would have to add one record for each of the lecturers on that course, and vice versa.
Put formally, there are two multivalued dependencies in this relation: {course}  {book} and equivalently {course}
{book} and equivalently {course}  {lecturer}.
{lecturer}.
Databases with multivalued dependencies thus exhibit redundancy. In database normalization, fourth normal form requires that either every multivalued dependency X  Y is trivial or for every nontrivial multivalued dependency X
Y is trivial or for every nontrivial multivalued dependency X  Y, X is a superkey. A multivalued dependency X
Y, X is a superkey. A multivalued dependency X  Y is trivial if Y is a subset of X, or if X and Y together form the whole set of attributes of the relation.
Y is trivial if Y is a subset of X, or if X and Y together form the whole set of attributes of the relation.
Properties
- If
 , Then
, Then 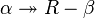
- If
 and
and 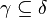 , Then
, Then 
- If
 and
and  , then
, then 
The following also involve functional dependencies:
- If
 , then
, then 
- If
 and
and  , then
, then 
The above rules are sound and complete.
- A decomposition of R into (X, Y) and (X, R − Y) is a lossless-join decomposition if and only if X
 Y holds in R.
Y holds in R. - Every FD is an MVD because if X
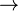 Y, then swapping Y's between tuples that agree on X doesn't create new tuples.
Y, then swapping Y's between tuples that agree on X doesn't create new tuples. - Splitting Doesn’t Hold. Like FD’s, we cannot generally split the left side of an MVD.But unlike FD’s, we cannot split the right side either, sometimes you have to leave several attributes on the right side.
- Closure of a set of MVDs is the set of all MVDs that can be inferred using the following rules (Armstrong's axioms):
- Complementation: If X
 Y, then X
Y, then X  R - XY
R - XY - Augmentation: If X
 Y and Z
Y and Z  W, then XW
W, then XW  YZ
YZ - Transitivity: If X
 Y and Y
Y and Y  Z, then X
Z, then X  Z - Y
Z - Y - Replication: If X
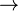 Y, then X
Y, then X  Y
Y - Coalescence: If X
 Y and
Y and  W s.t. W
W s.t. W  Y =
Y =  , W
, W 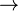 Z, and Z
Z, and Z  Y, then X
Y, then X 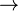 Z
Z
- Complementation: If X
Definitions
- full constraint
- A constraint which expresses something about all attributes in a database. (In contrast to an embedded constraint.) That a multivalued dependency is a full constraint follows from its definition,as where it says something about the attributes
 .
. - tuple-generating dependency
- A dependency which explicitly requires certain tuples to be present in the relation.
- trivial multivalued dependency 1
- A multivalued dependency which involves all the attributes of a relation i.e.
 . A trivial multivalued dependency implies, for tuples
. A trivial multivalued dependency implies, for tuples 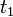 and
and  , tuples
, tuples 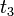 and
and  which are equal to
which are equal to 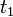 and
and  .
. - trivial multivalued dependency 2
- A multivalued dependency for which
 .
.
References
- ↑ Silberschatz, Abraham; Korth, Sudarshan (2006). Database System Concepts (5th ed.). McGraw-Hill. p. 295. ISBN 0-07-124476-X.
External links
- Multivalued dependencies and a new Normal form for Relational Databases (PDF) - Ronald Fagin, IBM Research Lab
- On the Structure of Armstrong Relations for Functional Dependencies (PDF) - CATRIEL BEERI (The Hebrew University), MARTIN DOWD (Rutgers University), RONALD FAGIN (IBM Research Laboratory) AND RICHARD STATMAN (Rutgers University)
- On a problem of Fagin concerning multivalued dependencies in relational databases (PDF) - Sven Hartmann, Massey University
![t _1[\alpha] = t _2 [\alpha] = t _3 [\alpha] = t _4 [\alpha]](../I/m/85dfa6c14b7eddaacd959fe36645bb7e.png)
![t _3[\beta] = t _1 [\beta]](../I/m/ca736f7724f1a97d2399cf73db719652.png)
![t _3[R - \beta] = t _2 [R - \beta]](../I/m/fcbff7e18df9591c9c1ed09355ea6014.png)
![t _4[\beta] = t _2 [\beta]](../I/m/a12ea64b17943932a37ad5453f927e86.png)
![t _4[R - \beta] = t _1 [R - \beta]](../I/m/0b5bda4e4851fe2b567c8be94ac569cc.png)