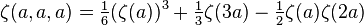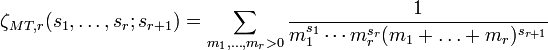Multiple zeta function
In mathematics, the multiple zeta functions are generalisations of the Riemann zeta function, defined by
and converge when Re(s1) + ... + Re(si) > i for all i. Like the Riemann zeta function, the multiple zeta functions can be analytically continued to be meromorphic functions (see, for example, Zhao (1999)). When s1, ..., sk are all positive integers (with s1 > 1) these sums are often called multiple zeta values (MZVs) or Euler sums.
The k in the above definition is named the "length" of a MZV, and the n = s1 + ... + sk is known as the "weight".[1]
The standard shorthand for writing multiple zeta functions is to place repeating strings of the argument within braces and use a superscript to indicate the number of repetitions. For example,
Two parameters case
In the particular case of only two parameters we have (with s>1 and n,m integer):[2]
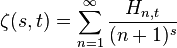 where
where 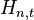 are the generalized harmonic numbers.
are the generalized harmonic numbers.
Multiple zeta functions are known to satisfy what is known as MZV duality, the simplest case of which is the famous identity of Euler:
where Hn are the harmonic numbers.
Special values of double zeta functions, with s > 0 and even, t > 1 and odd, but s+t=2N+1 (taking if necessary ζ(0) = 0):[2]
| s | t | approximate value | explicit formulae | OEIS |
|---|---|---|---|---|
| 2 | 2 | 0.811742425283353643637002772406 | 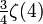 | |
| 3 | 2 | 0.228810397603353759768746148942 | 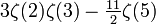 | |
| 4 | 2 | 0.088483382454368714294327839086 | 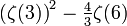 | |
| 5 | 2 | 0.038575124342753255505925464373 | 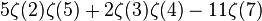 | |
| 6 | 2 | 0.017819740416835988 | ||
| 2 | 3 | 0.711566197550572432096973806086 | 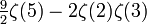 | |
| 3 | 3 | 0.213798868224592547099583574508 | 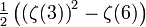 | |
| 4 | 3 | 0.085159822534833651406806018872 | 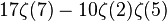 | |
| 5 | 3 | 0.037707672984847544011304782294 | 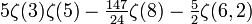 | |
| 2 | 4 | 0.674523914033968140491560608257 | 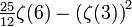 | |
| 3 | 4 | 0.207505014615732095907807605495 | 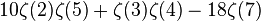 | |
| 4 | 4 | 0.083673113016495361614890436542 | 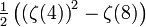 |
Note that if 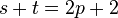 we have
we have 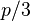 irreducibles, i.e. these MZVs cannot be written as function of
irreducibles, i.e. these MZVs cannot be written as function of 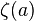 only.[3]
only.[3]
Three parameters case
In the particular case of only three parameters we have (with a>1 and n,j,i integer):
Euler reflection formula
The above MZVs satisfy the Euler reflection formula:
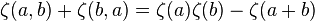 for
for 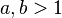
Using the shuffle relations, it is easy to prove that:[3]
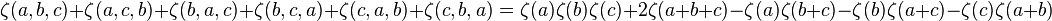 for
for 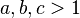
This function can be seen as a generalization of the reflection formulas.
Symmetric sums in terms of the zeta function
Let 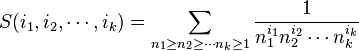 , and for a partition
, and for a partition 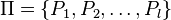 of the set
of the set 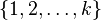 , let
, let 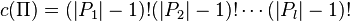 . Also, given such a
. Also, given such a  and a k-tuple
and a k-tuple 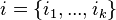 of exponents, define
of exponents, define 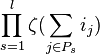 .
.
The relations between the 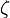 and
and 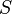 are:
are:
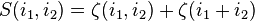 and
and 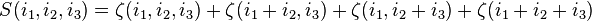
Theorem 1(Hoffman)
For any real 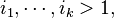 ,
,  .
.
Proof. Assume the 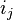 are all distinct. (There is not loss of generality, since we can take limits.) The left-hand side can be written as
are all distinct. (There is not loss of generality, since we can take limits.) The left-hand side can be written as
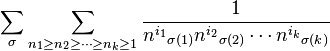 . Now thinking on the symmetric
. Now thinking on the symmetric
group 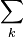 as acting on k-tuple
as acting on k-tuple 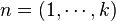 of positive integers. A given k-tuple
of positive integers. A given k-tuple 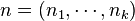 has an isotropy group
has an isotropy group
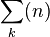 and an associated partition
and an associated partition 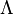 of
of 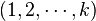 :
: 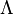 is the set of equivalence classes of the relation
given by
is the set of equivalence classes of the relation
given by 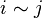 iff
iff 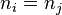 , and
, and 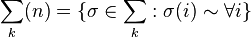 . Now the term
. Now the term 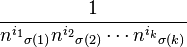 occurs on the left-hand side of
occurs on the left-hand side of  exactly
exactly 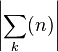 times. It occurs on the right-hand side in those terms corresponding to partitions
times. It occurs on the right-hand side in those terms corresponding to partitions  that are refinements of
that are refinements of 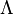 : letting
: letting  denote refinement,
denote refinement, 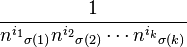 occurs
occurs 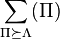 times. Thus, the conclusion will follow if
times. Thus, the conclusion will follow if
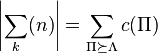 for any k-tuple
for any k-tuple 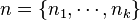 and associated partition
and associated partition 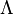 .
To see this, note that
.
To see this, note that 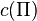 counts the permutations having cycle-type specified by
counts the permutations having cycle-type specified by  : since any elements of
: since any elements of 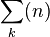 has a unique cycle-type specified by a partition that refines
has a unique cycle-type specified by a partition that refines 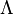 , the result follows.[4]
, the result follows.[4]
For  , the theorem says
, the theorem says 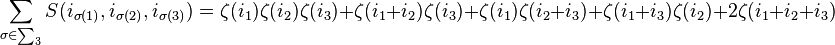 for
for 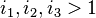 . This is the main result of.[5]
. This is the main result of.[5]
Having 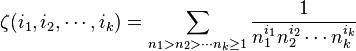 . To state the analog of Theorem 1 for the
. To state the analog of Theorem 1 for the 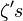 , we require one bit of notation. For a partition
, we require one bit of notation. For a partition
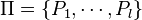 or
or 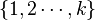 , let
, let 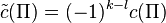 .
.
Theorem 2(Hoffman)
For any real 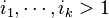 ,
,  .
.
Proof. We follow the same line of argument as in the preceding proof. The left-hand side is now
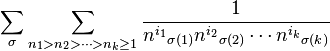 , and a term
, and a term 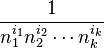 occurs on the left-hand since once if all the
occurs on the left-hand since once if all the 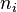 are distinct, and not at all otherwise. Thus, it suffices to show
are distinct, and not at all otherwise. Thus, it suffices to show
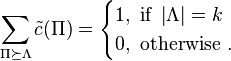 (1)
(1)
To prove this, note first that the sign of 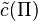 is positive if the permutations of cycle-type
is positive if the permutations of cycle-type  are even, and negative if they are odd: thus, the left-hand side of (1) is the signed sum of the number of even and odd permutations in the isotropy group
are even, and negative if they are odd: thus, the left-hand side of (1) is the signed sum of the number of even and odd permutations in the isotropy group 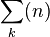 . But such an isotropy group has equal numbers of even and odd permutations unless it is trivial, i.e. unless the associated partition
. But such an isotropy group has equal numbers of even and odd permutations unless it is trivial, i.e. unless the associated partition 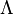 is
is
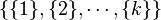 .[4]
.[4]
The sum and duality conjectures[4]
We first state the sum conjecture, which is due to C. Moen.[6]
Sum conjecture(Hoffman). For positive integers k and n,
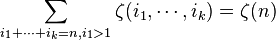 , where the sum is extended over k-tuples
, where the sum is extended over k-tuples 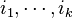 of positive integers with
of positive integers with 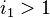 .
.
Three remarks concerning this conjecture are in order. First, it implies
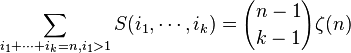 . Second, in the case
. Second, in the case  it says that
it says that 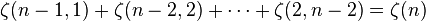 , or using the relation between the
, or using the relation between the 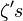 and
and 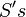 and Theorem 1,
and Theorem 1, 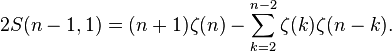
This was proved by Euler's paper[7] and has been rediscovered several times, in particular by Williams.[8] Finally, C. Moen[6] has proved the same conjecture for k=3 by lengthy but elementary arguments.
For the duality conjecture, we first define an involution 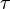 on the set
on the set 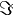 of finite sequences of positive integers whose first element is greater than 1. Let
of finite sequences of positive integers whose first element is greater than 1. Let 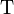 be the set of strictly increasing finite sequences of positive integers, and let
be the set of strictly increasing finite sequences of positive integers, and let 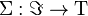 be the function that sends a sequence in
be the function that sends a sequence in 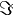 to its sequence of partial sums. If
to its sequence of partial sums. If 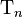 is the set of sequences in
is the set of sequences in 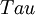 whose last element is at most
whose last element is at most  , we have two commuting involutions
, we have two commuting involutions  and
and  on
on 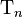 defined by
defined by
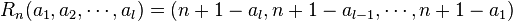 and
and
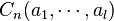 = complement of
= complement of 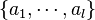 in
in 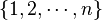 arranged in increasing order. The our definition of
arranged in increasing order. The our definition of 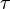 is
is 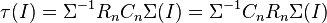 for
for 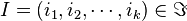 with
with 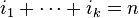 .
.
For example,
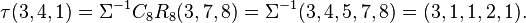 We shall say the sequences
We shall say the sequences 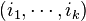 and
and 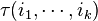 are dual to each other, and refer to a sequence fixed by
are dual to each other, and refer to a sequence fixed by 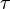 as self-dual.[4]
as self-dual.[4]
Duality conjecture (Hoffman). If 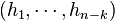 is dual to
is dual to 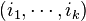 , then
, then 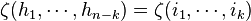 .
.
This sum conjecture is also known as Sum Theorem, and it may be expressed as follows: the Riemann zeta value of an integer n ≥ 2 is equal to the sum of all the valid (i.e. with s1 > 1) MZVs of the partitions of length k and weight n, with 1 ≤ k ≤n − 1. In formula:[1]
For example with length k = 2 and weight n = 7:
Euler sum with all possible alternations of sign
The Euler sum with alternations of sign appears in studies of the non-alternating Euler sum.[3]
Notation
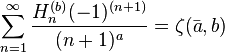 with
with 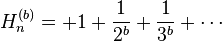 are the generalized harmonic numbers.
are the generalized harmonic numbers.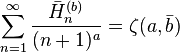 with
with 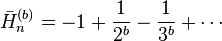
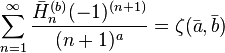
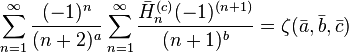 with
with 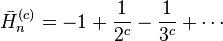
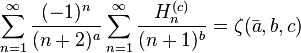 with
with 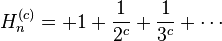
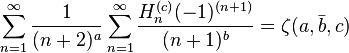
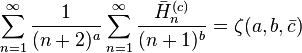
As a variant of the Dirichlet eta function we define
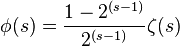 with
with 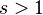
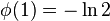
Reflection formula
The reflection formula 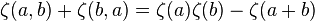 can be generalized as follows:
can be generalized as follows:
if 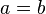 we have
we have ![\zeta(\bar{a},\bar{a})=\tfrac{1}{2}\Big[\phi^2(a)-\zeta(2a)\Big]](../I/m/5296a48391cb350b9c2732713c3a9b1f.png)
Other relations
Using the series definition it is easy to prove:
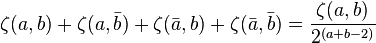 with
with 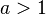
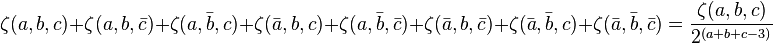 with
with 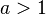
A further useful relation is:[3]
where ![Z_a(s,t)=\zeta(s,t)+\zeta(\bar{s},t)-\frac{\Big[\zeta(s,t)+\zeta(s+t)\Big]}{2^{(s-1)}}](../I/m/18ba0ab236ef1b9b72bd130494f3ba74.png) and
and 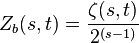
Note that  must be used for all value
must be used for all value  for whom the argument of the factorials is
for whom the argument of the factorials is 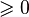
Other results
For any integer positive :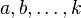 :
:
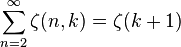 or more generally:
or more generally: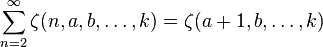
Mordell–Tornheim zeta values
The Mordell–Tornheim zeta function, introduced by Matsumoto (2003) who was motivated by the papers Mordell (1958) and Tornheim (1950), is defined by
It is a special case of the Shintani zeta function.
References
- Tornheim, Leonard (1950). "Harmonic double series". American Journal of Mathematics 72: 303–314. doi:10.2307/2372034. ISSN 0002-9327. MR 0034860.
- Mordell, Louis J. (1958). "On the evaluation of some multiple series". Journal of the London Mathematical Society. Second Series 33: 368–371. doi:10.1112/jlms/s1-33.3.368. ISSN 0024-6107. MR 0100181.
- Apostol, Tom M.; Vu, Thiennu H. (1984), "Dirichlet series related to the Riemann zeta function", Journal of Number Theory 19 (1): 85–102, doi:10.1016/0022-314X(84)90094-5, ISSN 0022-314X, MR 0751166
- Crandall, Richard E.; Buhler, Joe P. (1994). "On the evaluation of Euler Sums". Experimental Mathematics 3 (4): 275. doi:10.1080/10586458.1994.10504297. MR 1341720.
- Borwein, Jonathan M.; Girgensohn, Roland (1996). "Evaluation of Triple Euler Sums". El. J. Combinat. 3 (1): #R23. MR 1401442.
- Flajolet, Philippe; Salvy, Bruno (1998). "Euler Sums and contour integral representations". Exp. Math. 7.
- Zhao, Jianqiang (1999). "Analytic continuation of multiple zeta functions". Proceedings of the American Mathematical Society 128 (5): 1275–1283. doi:10.1090/S0002-9939-99-05398-8. MR 1670846.
- Matsumoto, Kohji (2003), "On Mordell–Tornheim and other multiple zeta-functions", Proceedings of the Session in Analytic Number Theory and Diophantine Equations, Bonner Math. Schriften 360, Bonn: Univ. Bonn, MR 2075634
- Espinosa, Olivier; Moll, Victor H. (2008). "The evaluation of Tornheim double sums". arXiv:0811.0557.
- Espinosa, Olivier; Moll, Victor H. (2010). "The evaluation of Tornheim double sums II". Ramanujan J. 22: 55–99. doi:10.1007/s11139-009-9181-1. MR 2610609.
- Borwein, J.M.; Chan, O-Y. (2010). "Duality in tails of multiple zeta values". Int. J. Number Theory 6 (3): 501–514. doi:10.1142/S1793042110003058. MR 2652893.
- Basu, Ankur (2011). "On the evaluation of Tornheim sums and allied double sums". Ramanujan J. 26 (2): 193–207. doi:10.1007/s11139-011-9302-5. MR 2853480.
Notes
- 1 2 Hoffman, Mike. "Multiple Zeta Values". Mike Hoffman's Home Page. U.S. Naval Academy. Retrieved June 8, 2012.
- 1 2 Borwein, David; Borwein, Jonathan; Bradley, David (September 23, 2004). "Parametric Euler Sum Identities" (PDF). CARMA, AMSI Honours Course. The University of Newcastle. Retrieved June 3, 2012.
- 1 2 3 4 Broadhurst, D. J. (1996). "On the enumeration of irreducible k-fold Euler sums and their roles in knot theory and field theory.". arXiv:hep-th/9604128.
- 1 2 3 4 Hoffman, Michael (1992). "Multiple Harmonic Series". Pacific Journal of Mathematics 152: 276–278. doi:10.2140/pjm.1992.152.275. MR 1141796. Zbl 0763.11037.
- ↑ Ramachandra Rao, R. Sita; M. V. Subbarao (1984). "Transformation formulae for multiple series". Pacific Journal of Mathematics 113: 417–479. doi:10.2140/pjm.1984.113.471.
- 1 2 Moen, C. "Sums of Simple Series". Preprint.
- ↑ Euler, L. (1775). "Meditationes circa singulare serierum genus". Novi Comm. Acad. Sci. Petropol 15 (20): 140–186.
- ↑ Williams, G. T. (1958). "On the evaluation of some multiple series". Journal of the London Mathematical Society 33: 368–371. doi:10.1112/jlms/s1-33.3.368.
External links
- Borwein, Jonathan; Zudilin, Wadim. "Lecture notes on the Multiple Zeta Function".
- Hoffman, Michael (2012). "Multiple zeta values".
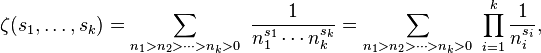
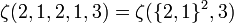
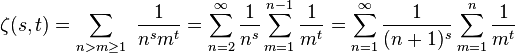
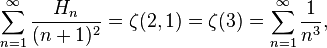
![\zeta(s,t)=\zeta(s)\zeta(t)+\tfrac{1}{2}\Big[\tbinom{s+t}{s}-1\Big]\zeta(s+t)-\sum_{r=1}^{N-1}\Big[\tbinom{2r}{s-1}+\tbinom{2r}{t-1}\Big]\zeta(2r+1)\zeta(s+t-1-2r)](../I/m/2a377306860dd65a4877db1c7abbee69.png)
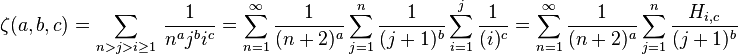
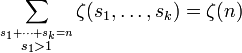
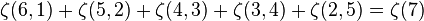
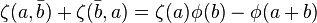
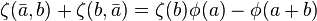
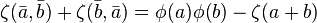
![\zeta(a,b)+\zeta(\bar{a},\bar{b})=\sum_{s>0} (a+b-s-1)!\Big[\frac{Z_a(a+b-s,s)}{(a-s)!(b-1)!}+\frac{Z_b(a+b-s,s)}{(b-s)!(a-1)!}\Big]](../I/m/c540846e453618a86ad7e307aa86571d.png)
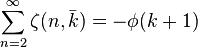
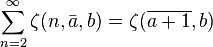
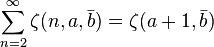
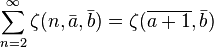
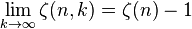
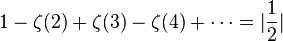
![\zeta(a,a)=\tfrac{1}{2}\Big[(\zeta(a))^{2}-\zeta(2a)\Big]](../I/m/684027e0d244679d0f236687e08217b5.png)