Multipartite entanglement
In the case of systems composed of  subsystems the classification of entangled states is richer than in the bipartite case. Indeed, in multipartite entanglement apart from fully separable states and fully entangled states, there also exists the notion of partially separable states.[1]
subsystems the classification of entangled states is richer than in the bipartite case. Indeed, in multipartite entanglement apart from fully separable states and fully entangled states, there also exists the notion of partially separable states.[1]
Full and partial separability
The definitions of fully separable and fully entangled multipartite states naturally generalizes that of separable and entangled states in the bipartite case, as follows.[1]
Definition [Full  -partite separability (
-partite separability ( -separability) of
-separability) of  systems]: The state
systems]: The state  of
of  subsystems
subsystems  with Hilbert space
with Hilbert space  is fully separable if and only if it can be written in the form
is fully separable if and only if it can be written in the form
Correspondingly, the state  is fully entangled if it cannot be written in the above form.
is fully entangled if it cannot be written in the above form.
As in the bipartite case, the set of  -separable states is convex and closed with respect to trace norm, and separability is preserved under
-separable states is convex and closed with respect to trace norm, and separability is preserved under  -separable operations
-separable operations  which are a straightforward generalization of the bipartite ones:
which are a straightforward generalization of the bipartite ones:
As mentioned above, though, in the multipartite setting we also have different notions of partial separability.[1]
Definition [separability with respect to partitions]: The state  of
of  subsystems
subsystems  is separable with respect to a given partition
is separable with respect to a given partition  , where
, where  are disjoint subsets of the indices
are disjoint subsets of the indices 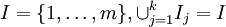 , if and only if it can be written
, if and only if it can be written
Definition [semiseparability]: The state  is semiseparable if and only if it is separable under all
is semiseparable if and only if it is separable under all 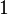 -
- partitions,
partitions,  .[1]
.[1]
Definition [s-particle entanglement]: An  -particle system can have at most
-particle system can have at most  -particle entanglement if it is a mixture of all states such that each of them is separable with respect to some partition
-particle entanglement if it is a mixture of all states such that each of them is separable with respect to some partition  , where all sets of indices
, where all sets of indices  have cardinality
have cardinality  .[1]
.[1]
Separability characterization and criteria
Pure states
An equivalent definition to Full m-partite separability is given as follows: The pure state  of
of  subsystems
subsystems  is fully
is fully  -partite separable if and only if it can be written
-partite separable if and only if it can be written
In order to check this, it is enough to compute reduced density matrices of elementary subsystems and see whether they are pure. However, this cannot be done so easily in the multipartite case, as only rarely multipartite pure states admit the generalized Schmidt Decomposition  . A multipartite state admits generalized Schmidt decomposition if, tracing out any subsystem, the rest is in a fully separable state.
Thus, in general the entanglement of a pure state is described by the spectra of the reduced density matrices of all bipartite partitions: the state is genuinely
. A multipartite state admits generalized Schmidt decomposition if, tracing out any subsystem, the rest is in a fully separable state.
Thus, in general the entanglement of a pure state is described by the spectra of the reduced density matrices of all bipartite partitions: the state is genuinely  -partite entangled if and only if all bipartite partitions produce mixed reduced density matrices.[1]
-partite entangled if and only if all bipartite partitions produce mixed reduced density matrices.[1]
Mixed states
In the multipartite case there is no simple necessary and sufficient condition for separability like the one given by the PPT criterion for the  and
and  cases. However, many separability criteria used in the bipartite setting can be generalized to the multipartite case.[1]
cases. However, many separability criteria used in the bipartite setting can be generalized to the multipartite case.[1]
Positive but not completely positive (PnCP) maps and entanglement witnesses
The characterization of separability in terms of positive but not completely positive maps can be naturally generalized from the bipartite case, as follows.[1]
Any positive but not completely positive (PnCP) map 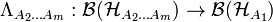 provides a nontrivial necessary separability criterion in the form:
provides a nontrivial necessary separability criterion in the form:
where  is the identity acting on the first subsystem
is the identity acting on the first subsystem  .
The state
.
The state  is separable if and only if the above condition is satisfied for all PnCP maps
is separable if and only if the above condition is satisfied for all PnCP maps 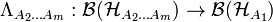 .[1]
.[1]
The definition of entanglement witnesses and the Choi-Jamiolkowski isomorphism that links PnCP maps to entanglement witnesses in the bipartite case can also be generalized to the multipartite setting.
We therefore get a separability condition from entanglement witnesses for multipartite states: the state  is separable if it has non-negative mean value
is separable if it has non-negative mean value  for all entanglement witnesses
for all entanglement witnesses 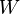 . Correspondingly, the entanglement of
. Correspondingly, the entanglement of  is detected by the witness
is detected by the witness 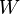 if and only if
if and only if  .[1]
.[1]
The above description provides a full characterization of  -separability of
-separability of  -partite systems.[1]
-partite systems.[1]
Range criterion
The "range criterion" can also be immediately generalized from the bipartite to the multipartite case. In the latter case the range of  must be spanned by the vectors
must be spanned by the vectors  , while the range of
, while the range of 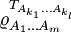 partially transposed with respect to the subset
partially transposed with respect to the subset  must be spanned by the products of these vectors where those with indices
must be spanned by the products of these vectors where those with indices  are complex conjugated. If the state
are complex conjugated. If the state  is separable, then all such partial transposes must lead to matrices with non-negative spectrum, i.e. all the matrices
is separable, then all such partial transposes must lead to matrices with non-negative spectrum, i.e. all the matrices 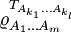 should be states themselves.[1]
should be states themselves.[1]
Realignment criteria
The "realignment criteria" from the bipartite case are generalized to permutational criteria in the multipartite setting: if the state 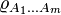 is separable, then the matrix
is separable, then the matrix ![\; [R_\pi(\varrho_{A_1\ldots A_m})]_{i_1j_1,i_2j_2,\ldots,i_nj_n}\equiv\varrho_{\pi(i_1j_1,i_2j_2,\ldots,i_nj_n)}](../I/m/f6ba69a8595002bd512d7ff18d013263.png) , obtained from the original state via permutation
, obtained from the original state via permutation  of matrix indices in product basis, satisfies
of matrix indices in product basis, satisfies ![\; ||R_\pi(\varrho_{A_1\ldots A_m})]||_{Tr}\leq1](../I/m/bccdec54fdf017b960910c883971740c.png) .[1]
.[1]
Contraction criterion
Finally, the contraction criterion generalizes immediately from the bipartite to the multipartite case.[1]
Multipartite entanglement measures
Many of the axiomatic entanglement measures for bipartite states, such as relative entropy of entanglement, robustness of entanglement and squashed entanglement can be generalized to the multipartite setting.[1]
The relative entropy of entanglement, for example, can be generalized to the multipartite case by taking a suitable set in place of the set of bipartite separable states. One can take the set of fully separable states, even though with this choice the measure will not distinguish between truly multipartite entanglement and several instances of bipartite entanglement, such as  . In order to analyze truly multipartite entanglement one has to consider the set of states containing no more than
. In order to analyze truly multipartite entanglement one has to consider the set of states containing no more than  -particle entanglement.[1]
-particle entanglement.[1]
In the case of squashed entanglement, its multipartite version can be obtained by simply replacing the mutual information of the bipartite system with its generalization for multipartite systems, i.e.
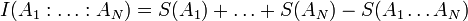 .[1]
.[1]
However, in the multipartite setting many more parameters are needed to describe the entanglement of the states, and therefore many new entanglement measures have been constructed, especially for pure multipartite states.
Multipartite entanglement measures for pure states
In the multipartite setting there are entanglement measures that simply are functions of sums of bipartite entanglement measures, as, for instance, the global entanglement, which is given by the sum of concurrences between one qubit and all others. For these multipartite entanglement measures the 'monotonicity under LOCC is simply inherited from the bipartite measures. But there are also entanglement measures that were constructed specifically for multipartite states, as the following:[1]
Tangle
The first multipartite entanglement measure that is neither a direct generalization nor an easy combination of bipartite measures was introduced by Coffman et al. and called tangle.[1]
Definition [tangle]:
where the  -tangles on the right-hand-side are the squares of concurrence.[1]
-tangles on the right-hand-side are the squares of concurrence.[1]
The tangle measure is permutationally invariant; it vanishes on all states that are separable under any cut; it is nonzero, for example, on the GHZ-state; it can be thought to be zero for states that are 3-entangled (i.e. that are not product with respect to any cut) as, for instance, the W-state. Moreover, there might be the possibility to obtain a good generalization of the tangle for multiqubit systems by means of hyperdeterminant.[1]
Schmidt measure
This was one of the first entanglement measures constructed specifically for multipartite states.[1]
Definition [Schmidt measure]: The minimum of  , where
, where  is the number of terms in an expansion of the state in product basis.[1]
is the number of terms in an expansion of the state in product basis.[1]
This measure is zero if and only if the state is fully product; therefore, it cannot distinguish between truly multipartite entanglement and bipartite entanglement, but it may nevertheless be useful in many contexts.[1]
Measures based on normal forms
This is an interesting class of multipartite entanglement measures obtained in the context of classification of states. Namely, one considers any homogeneous function of the state: if it is invariant under SLOCC (stochastic LOCC) operations with determinant equal to 1, then it is an entanglement monotone in the strong sense, i.e. it satisfies the condition of strong monotonicity.[1]
Measures based on hyperdeterminant
It was proved by Miyake that hyperdeterminants are entanglement monotones and they describe truly multipartite entanglement in the sense that states such as products of  's have zero entanglement. In particular concurrence and tangle are special cases of hyperdeterminant. Indeed for two qubits concurrence is simply the modulus of the determinant, which is the hyperdeterminant of first order; whereas the tangle is the hyperdeterminant of second order, i.e. a function of tensors with three indices.[1]
's have zero entanglement. In particular concurrence and tangle are special cases of hyperdeterminant. Indeed for two qubits concurrence is simply the modulus of the determinant, which is the hyperdeterminant of first order; whereas the tangle is the hyperdeterminant of second order, i.e. a function of tensors with three indices.[1]
Geometric entanglement
Definition [geometric entanglement]:
where ![\; \Lambda^k[\psi] = sup_{\phi \in S_k}|\langle \psi|\phi\rangle|^2](../I/m/8b92252d9a0b11b978c4ad6dd34112e6.png) , with
, with  the set of
the set of 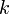 -separable states. This measure belongs to a family of entanglement measures defined by Barnum and Linden, and it is the multipartite generalization of the Shimony measure.[1]
-separable states. This measure belongs to a family of entanglement measures defined by Barnum and Linden, and it is the multipartite generalization of the Shimony measure.[1]
Localisable entanglement
This entanglement measure is a generalization of the entanglement of assistance and was constructed in the context of spin chains. Namely, one chooses two spins and performs LOCC operations that aim at obtaining the largest possible bipartite entanglement between them (measured according to a chosen entanglement measure for two bipartite states).[1]
Sources and notes
Further reading
- Horodecki, R. (1994). "Informationally coherent quantum systems". Physics Letters A 187 (2): 145. Bibcode:1994PhLA..187..145H. doi:10.1016/0375-9601(94)90052-3.
- Coffman, V.; Kundu, Joydip; Wootters, William K. (2000). "Distributed entanglement". Physical Review A 61 (5): 052306. arXiv:quant-ph/9907047. Bibcode:2000PhRvA..61e2306C. doi:10.1103/PhysRevA.61.052306.
- Barnum, H.; Linden, N. (2001). "Monotones and invariants for multi-particle quantum states". Journal of Physics A 34 (35): 6787. arXiv:quant-ph/0103155. Bibcode:2001JPhA...34.6787B. doi:10.1088/0305-4470/34/35/305.
- Bourennane, M.; Karlsson, A.; Björk, G. (2001). "Quantum key distribution using multilevel encoding". Physical Review A 64 (2): 022306. Bibcode:2001PhRvA..64a2306B. doi:10.1103/PhysRevA.64.012306.
- Meyer, D. A.; Wallach, N. R. (2001). "Global entanglement in multiparticle systems". arXiv:quant-ph/0108104 [quant-ph].
- Miyake, A. (2003). "Classification of multipartite entangled states by multidimensional determinants". Physical Review A 67 (1): 012108. arXiv:quant-ph/0206111. Bibcode:2003PhRvA..67a2108M. doi:10.1103/PhysRevA.67.012108.
- Verstraete, F.; Dehaene, J.; De Moor, B. (2003). "Normal forms and entanglement measures for multipartite quantum states". Physical Review A 68 (1): 012103. arXiv:quant-ph/0105090. Bibcode:2003PhRvA..68a2103V. doi:10.1103/PhysRevA.68.012103.
- Boileau, J.-C.; Gottesman, D.; Laflamme, R.; Poulin, D.; Spekkens, R. (2004). "Robust Polarization-Based Quantum Key Distribution over a Collective-Noise Channel". Physical Review Letters 92 (2): 027901. arXiv:quant-ph/0306199. Bibcode:2004PhRvL..92a7901B. doi:10.1103/PhysRevLett.92.017901.
- Miyake, A. (2004). "Multipartite Entanglement under Stochastic Local Operations and Classical Communication". International Journal of Quantum Information 2: 65. arXiv:quant-ph/0401023. Bibcode:2004quant.ph..1023M.
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. (2009). "Quantum entanglement". Reviews of Modern Physics 81 (2): 865–942. arXiv:quant-ph/0702225. Bibcode:2009RvMP...81..865H. doi:10.1103/RevModPhys.81.865.
- Gühne, O.; Tóth, G. (2009). "Entanglement detection". Physics Reports 474: 1–75. arXiv:0811.2803. Bibcode:2009PhR...474....1G. doi:10.1016/j.physrep.2009.02.004.

![\; \varrho_{A_1\ldots A_m}\to
\frac{\sum_i\Omega_i^1\otimes\ldots\otimes\Omega_i^n\varrho_{A_1\ldots A_m}
(\Omega_i^1\otimes\ldots\otimes\Omega_i^n)^\dagger}{Tr[\sum_i
\Omega_i^1\otimes\ldots\otimes\Omega_i^n\varrho_{A_1\ldots A_m}
(\Omega_i^1\otimes\ldots\otimes\Omega_i^n)^\dagger]} .](../I/m/a2f9567ba864efb6e0348d000eea65e7.png)


![\; (I_{A_1}\otimes \Lambda_{A_2\ldots A_m})[\varrho_{A_1\ldots A_m}] \geq 0 ,](../I/m/7e10f171775348c0fab1a196060a8055.png)
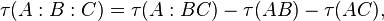
![\; E_g = 1 - \Lambda^k[\psi] ,](../I/m/af24ca1cb845ed1f0025498d2e3f5318.png)