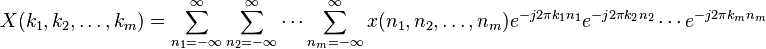Multidimensional signal processing

In signal processing, multidimensional signal processing covers all signal processing done using multidimensional signals and systems. While multidimensional signal processing is a subset of signal processing, it is unique in the sense that it deals specifically with data that can only be adequately detailed using more than one dimension. In m-D digital signal processing, useful data is sampled in more than one dimension. Examples of this are image processing and multi-sensor radar detection. Both of these examples use multiple sensors to sample signals and form images based on the manipulation of these multiple signals. Processing in multi-dimension (m-D) requires more complex algorithms, compared to the 1-D case, to handle calculations such as the Fast Fourier Transform due to more degrees of freedom.[1] In some cases, m-D signals and systems can be simplified into single dimension signal processing methods, if the considered systems are separable.

Typically, multidimensional signal processing is directly associated with digital signal processing because its complexity warrants the use of computer modelling and computation.[1] A multidimensional signal is similar to a single dimensional signal as far as manipulations that can be performed, such as sampling, Fourier analysis, and filtering. The actual computations of these manipulations grow with the number of dimensions.

Sampling

Multidimensional sampling requires different analysis than typical 1-D sampling. Single dimension sampling is executed by selecting points along a continuous line and storing the values of this data stream. In the case of multidimensional sampling, the data is selected utilizing a lattice, which is a "pattern" based on the sampling vectors of the m-D data set.[2] These vectors can be single dimensional or multidimensional depending on the data and the application.[2]

Multidimensional sampling is similar to classical sampling as it must adhere to the Nyquist–Shannon sampling theorem. It is affected by aliasing and considerations must be made for eventual reconstruction.

Fourier Analysis

A multidimensional signal can be represented in terms of sinusoidal components. This is typically done with a type of Fourier transform. The m-D Fourier transform transforms a signal from a signal domain representation to a frequency domain representation of the signal. In the case of digital processing, a discrete Fourier Transform (DFT) is utilized to transform a sampled signal domain representation into a frequency domain representation:

X(k_1,k_2,\dots,k_m) = \sum_{n_1=-\infty}^\infty \sum_{n_2=-\infty}^\infty \cdots \sum_{n_m=-\infty}^\infty x(n_1,n_2,\dots,n_m) e^{-j 2 \pi k_1 n_1} e^{-j 2 \pi k_2 n_2} \cdots e^{-j 2 \pi k_m n_m}

where X stands for the multidimensional discrete Fourier transform, x stands for the sampled time/space domain signal, m stands for the number of dimensions in the system, n are sample indices and k are frequency samples.[3] Computational complexity is usually the main concern when implementing any Fourier transform. For multidimensional signals, the complexity can be reduced by a number of different methods. The computation may be simplified if there is independence between variables of the multidimensional signal.[3] In general, Fast Fourier Transforms (FFTs), reduce the number of computations by a substantial factor. While there are a number of different implementations of this algorithm for m-D signals, two often used variations are the vector-radix FFT and the row-column FFT.

Filtering

A 2-D filter (left) defined by its 1-D prototype function (right) and a McClellan transformation.

Filtering is an important part of any signal processing application. Similar to typical single dimension signal processing applications, there are varying degrees of complexity within filter design for a given system. M-D systems utilize digital filters in many different applications. The actual implementation of these m-D filters can pose a design problem depending on whether the multidimensional polynomial is factorable.[3] Typically, a prototype filter is designed in a single dimension and that filter is extrapolated to m-D using a mapping function.[3] One of the original mapping functions from 1-D to 2-D was the McClellan Transform.[4] Both FIR and IIR filters can be transformed to m-D, depending on the application and the mapping function.

Applicable Fields

References

  1. 1 2 D. Dudgeon and R. Mersereau, Multidimensional Digital Signal Processing, Prentice-Hall, First Edition, pp. 2, 1983.
  2. 1 2 Mersereau, R.; Speake, T., "The processing of periodically sampled multidimensional signals," Acoustics, IEEE Transactions on Speech and Signal Processing, vol.31, no.1, pp.188-194, Feb 1983.
  3. 1 2 3 4 D. Dudgeon and R. Mersereau, Multidimensional Digital Signal Processing, Prentice-Hall, First Edition, pp. 61,112, 1983.
  4. ↑ Mersereau, R.M.; Mecklenbrauker, W.; Quatieri, T., Jr., "McClellan transformations for two-dimensional digital filtering-Part I: Design," IEEE Transactions on Circuits and Systems, vol.23, no.7, pp.405-414, Jul 1976.
This article is issued from Wikipedia - version of the Sunday, January 31, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.