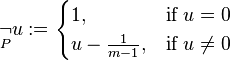Many-valued logic
In logic, a many-valued logic (also multi- or multiple-valued logic) is a propositional calculus in which there are more than two truth values. Traditionally, in Aristotle's logical calculus, there were only two possible values (i.e., "true" and "false") for any proposition. Classical two-valued logic may be extended to n-valued logic for n greater than 2. Those most popular in the literature are three-valued (e.g., Łukasiewicz's and Kleene's, which accept the values "true", "false", and "unknown"), the finite-valued (finitely-many valued) with more than three values, and the infinite-valued (infinitely-many valued), such as fuzzy logic and probability logic.
History
The first known classical logician who didn't fully accept the law of excluded middle was Aristotle (who, ironically, is also generally considered to be the first classical logician and the "father of logic"[1]). Aristotle admitted that his laws did not all apply to future events (De Interpretatione, ch. IX), but he didn't create a system of multi-valued logic to explain this isolated remark. Until the coming of the 20th century, later logicians followed Aristotelian logic, which includes or assumes the law of the excluded middle.
The 20th century brought back the idea of multi-valued logic. The Polish logician and philosopher Jan Łukasiewicz began to create systems of many-valued logic in 1920, using a third value, "possible", to deal with Aristotle's paradox of the sea battle. Meanwhile, the American mathematician, Emil L. Post (1921), also introduced the formulation of additional truth degrees with n ≥ 2, where n are the truth values. Later, Jan Łukasiewicz and Alfred Tarski together formulated a logic on n truth values where n ≥ 2. In 1932 Hans Reichenbach formulated a logic of many truth values where n→∞. Kurt Gödel in 1932 showed that intuitionistic logic is not a finitely-many valued logic, and defined a system of Gödel logics intermediate between classical and intuitionistic logic; such logics are known as intermediate logics.
Examples
Kleene (strong) K3 and Priest logic P3
Kleene's "(strong) logic of indeterminacy" K3 (sometimes 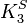 ) and Priest's "logic of paradox" add a third "undefined" or "indeterminate" truth value I. The truth functions for negation (¬), conjunction (∧), disjunction (∨), implication (), and biconditional () are given by:[2]
) and Priest's "logic of paradox" add a third "undefined" or "indeterminate" truth value I. The truth functions for negation (¬), conjunction (∧), disjunction (∨), implication (), and biconditional () are given by:[2]
|
|
|
|
|
The difference between the two logics lies in how tautologies are defined. In K3 only T is a designated truth value, while in P3 both T and I are (a logical formula is considered a tautology if it evaluates to a designated truth value). In Kleene's logic I can be interpreted as being "underdetermined", being neither true nor false, while in Priest's logic I can be interpreted as being "overdetermined", being both true and false. K3 does not have any tautologies, while P3 has the same tautologies as classical two-valued logic.
Bochvar's internal three-valued logic (also known as Kleene's weak three-valued logic)
Another logic is Bochvar's "internal" three-valued logic ( ) also called Kleene's weak three-valued logic. Except for negation and biconditional, its truth tables are all different from the above.[3]
) also called Kleene's weak three-valued logic. Except for negation and biconditional, its truth tables are all different from the above.[3]
|
|
|
The intermediate truth value in Bochvar's "internal" logic can be described as "contagious" because it propagates in a formula regardless of the value of any other variable.[4]
Belnap logic (B4)
Belnap's logic B4 combines K3 and P3. The overdetermined truth value is here denoted as B and the underdetermined truth value as N.
|
|
|
Gödel logics Gk and G∞
In 1932 Gödel defined[5] a family 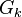 of many-valued logics, with finitely many truth values
of many-valued logics, with finitely many truth values 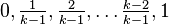 , for example
, for example  has the truth values
has the truth values 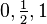 and
and  has
has 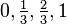 . In a similar manner he defined a logic with infinitely many truth values,
. In a similar manner he defined a logic with infinitely many truth values,  , in which the truth values are all the real numbers in the interval
, in which the truth values are all the real numbers in the interval ![[0,1]](../I/m/ccfcd347d0bf65dc77afe01a3306a96b.png) . The designated truth value in these logics is 1.
. The designated truth value in these logics is 1.
The conjunction 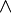 and the disjunction
and the disjunction  are defined respectively as the maximum and minimum of the operands:
are defined respectively as the maximum and minimum of the operands:
Negation 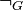 and implication
and implication ![\xrightarrow[G]{}](../I/m/24beca3771dd3e9d3e5d89dc9355bee9.png) are defined as follows:
are defined as follows:
Gödel logics are completely axiomatisable, that is to say it is possible to define a logical calculus in which all tautologies are provable.
Łukasiewicz logics Lv and L∞
Implication ![\xrightarrow[L]{}](../I/m/188b9ff275504af0fb6419ad96533b17.png) and negation
and negation  were defined by Jan Łukasiewicz through the following functions:
were defined by Jan Łukasiewicz through the following functions:
At first Łukasiewicz used these definition in 1920 for his three-valued logic  , with truth values
, with truth values 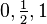 . In 1922 he developed a logic with infinitely many values
. In 1922 he developed a logic with infinitely many values 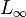 , in which the truth values spanned the real numbers in the interval
, in which the truth values spanned the real numbers in the interval ![[0,1]](../I/m/ccfcd347d0bf65dc77afe01a3306a96b.png) . In both cases the designated truth value was 1.[6]
. In both cases the designated truth value was 1.[6]
By adopting truth values defined in the same way as for Gödel logics 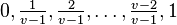 , it is possible to create a finitely-valued family of logics
, it is possible to create a finitely-valued family of logics  , the abovementioned
, the abovementioned 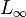 and the logic
and the logic 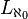 , in which the truth values are given by the rational numbers in the interval
, in which the truth values are given by the rational numbers in the interval ![[0,1]](../I/m/ccfcd347d0bf65dc77afe01a3306a96b.png) . The set of tautologies in
. The set of tautologies in 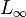 and
and 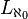 is identical.
is identical.
Product logic Π
In product logic we have truth values in the interval ![[0,1]](../I/m/ccfcd347d0bf65dc77afe01a3306a96b.png) , a conjunction
, a conjunction 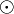 and an implication
and an implication ![\xrightarrow [\Pi]{}](../I/m/0829d53cae0acdb7b839f0fa8bc845ab.png) , defined as follows[7]
, defined as follows[7]
Additionally there is a negative designated value 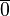 that denotes the concept of false. Through this value it is possible to define a negation
that denotes the concept of false. Through this value it is possible to define a negation 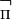 and an additional conjunction
and an additional conjunction 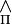 as follows:
as follows:
Post logics Pm
In 1921 Post defined a family of logics 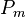 with (as in
with (as in  and
and 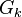 ) the truth values
) the truth values 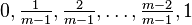 . Negation
. Negation 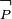 and disjunction
and disjunction  are defined as follows:
are defined as follows:
Semantics
Matrix semantics (logical matrices)
See Logical matrix
Relation to classical logic
Logics are usually systems intended to codify rules for preserving some semantic property of propositions across transformations. In classical logic, this property is "truth." In a valid argument, the truth of the derived proposition is guaranteed if the premises are jointly true, because the application of valid steps preserves the property. However, that property doesn't have to be that of "truth"; instead, it can be some other concept.
Multi-valued logics are intended to preserve the property of designationhood (or being designated). Since there are more than two truth values, rules of inference may be intended to preserve more than just whichever corresponds (in the relevant sense) to truth. For example, in a three-valued logic, sometimes the two greatest truth-values (when they are represented as e.g. positive integers) are designated and the rules of inference preserve these values. Precisely, a valid argument will be such that the value of the premises taken jointly will always be less than or equal to the conclusion.
For example, the preserved property could be justification, the foundational concept of intuitionistic logic. Thus, a proposition is not true or false; instead, it is justified or flawed. A key difference between justification and truth, in this case, is that the law of excluded middle doesn't hold: a proposition that is not flawed is not necessarily justified; instead, it's only not proven that it's flawed. The key difference is the determinacy of the preserved property: One may prove that P is justified, that P is flawed, or be unable to prove either. A valid argument preserves justification across transformations, so a proposition derived from justified propositions is still justified. However, there are proofs in classical logic that depend upon the law of excluded middle; since that law is not usable under this scheme, there are propositions that cannot be proven that way.
Suszko's thesis
Applications
Known applications of many-valued logic can be roughly classified into two groups.[8] The first group uses many-valued logic domain to solve binary problems more efficiently. For example, a well-known approach to represent a multiple-output Boolean function is to treat its output part as a single many-valued variable and convert it to a single-output characteristic function. Other applications of many-valued logic include design of Programmable Logic Arrays (PLAs) with input decoders, optimization of finite state machines, testing, and verification.
The second group targets the design of electronic circuits which employ more than two discrete levels of signals, such as many-valued memories, arithmetic circuits, Field Programmable Gate Arrays (FPGA) etc. Many-valued circuits have a number of theoretical advantages over standard binary circuits. For example, the interconnect on and off chip can be reduced if signals in the circuit assume four or more levels rather than only two. In memory design, storing two instead of one bit of information per memory cell doubles the density of the memory in the same die size. Applications using arithmetic circuits often benefit from using alternatives to binary number systems. For example, residue and redundant number systems[9] can reduce or eliminate the ripple-through carries which are involved in normal binary addition or subtraction, resulting in high-speed arithmetic operations. These number systems have a natural implementation using many-valued circuits. However, the practicality of these potential advantages heavily depends on the availability of circuit realizations, which must be compatible or competitive with present-day standard technologies.
Research venues
An IEEE International Symposium on Multiple-Valued Logic (ISMVL) has been held annually since 1970. It mostly caters to applications in digital design and verification.[10] There is also a Journal of Multiple-Valued Logic and Soft Computing.[11]
See also
- Mathematical logic
- Degrees of truth
- Fuzzy logic
- Gödel logic
- Kleene logic
- Kleene algebra (with involution)
- Łukasiewicz logic
- MV-algebra
- Post logic
- Principle of bivalence
- A. N. Prior
- Relevance logic
- Philosophical logic
- Digital logic
- MVCML, multiple-valued current-mode logic
- IEEE 1164 a nine-valued standard for VHDL
- IEEE 1364 a four-valued standard for Verilog
- Three-state logic
- Noise-based logic
Notes
References
- ↑ Hurley, Patrick. A Concise Introduction to Logic, 9th edition. (2006).
- ↑ (Gottwald 2005, p. 19)
- ↑ (Bergmann 2008, p. 80)
- ↑ (Bergmann 2008, p. 80)
- ↑ Gödel, Kurt (1932). "Zum intuitionistischen Aussagenkalkül". Anzeiger Akademie der Wissenschaften Wien (69): 65f.
- ↑ Kreiser, Lothar; Gottwald, Siegfried; Stelzner, Werner (1990). Nichtklassische Logik. Eine Einführung. Berlin: Akademie-Verlag. pp. 41ff –– 45ff. ISBN 978-3-05-000274-3.
- ↑ Hajek, Petr: Fuzzy Logic. In: Edward N. Zalta: The Stanford Encyclopedia of Philosophy, Spring 2009. ()
- ↑ Dubrova, Elena (2002). Multiple-Valued Logic Synthesis and Optimization, in Hassoun S. and Sasao T., editors, Logic Synthesis and Verification, Kluwer Academic Publishers, pp. 89-114
- ↑ Meher, Pramod Kumar; Valls, Javier; Juang, Tso-Bing; Sridharan, K.; Maharatna, Koushik (2008-08-22). "50 Years of CORDIC: Algorithms, Architectures and Applications" (PDF). IEEE Transactions on Circuits & Systems-I: Regular Papers (2009-09-09) 56 (9): 1893–1907. Retrieved 2016-01-03.
- ↑ http://www.informatik.uni-trier.de/~ley/db/conf/ismvl/index.html
- ↑ http://www.oldcitypublishing.com/MVLSC/MVLSC.html
Further reading
General
- Béziau J.-Y. (1997), What is many-valued logic ? Proceedings of the 27th International Symposium on Multiple-Valued Logic, IEEE Computer Society, Los Alamitos, pp. 117–121.
- Malinowski, Gregorz, (2001), Many-Valued Logics, in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic. Blackwell.
- Bergmann, Merrie (2008), An introduction to many-valued and fuzzy logic: semantics, algebras, and derivation systems, Cambridge University Press, ISBN 978-0-521-88128-9
- Cignoli, R. L. O., D'Ottaviano, I, M. L., Mundici, D., (2000). Algebraic Foundations of Many-valued Reasoning. Kluwer.
- Malinowski, Grzegorz (1993). Many-valued logics. Clarendon Press. ISBN 978-0-19-853787-8.
- S. Gottwald, A Treatise on Many-Valued Logics. Studies in Logic and Computation, vol. 9, Research Studies Press: Baldock, Hertfordshire, England, 2001.
- Gottwald, Siegfried (2005). "Many-Valued Logics" (PDF).
- Miller, D. Michael; Thornton, Mitchell A. (2008). Multiple valued logic: concepts and representations. Synthesis lectures on digital circuits and systems 12. Morgan & Claypool Publishers. ISBN 978-1-59829-190-2.
- Hájek P., (1998), Metamathematics of fuzzy logic. Kluwer. (Fuzzy logic understood as many-valued logic sui generis.)
Specific
- Alexandre Zinoviev, Philosophical Problems of Many-Valued Logic, D. Reidel Publishing Company, 169p., 1963.
- Prior A. 1957, Time and Modality. Oxford University Press, based on his 1956 John Locke lectures
- Goguen J.A. 1968/69, The logic of inexact concepts, Synthese, 19, 325–373.
- Chang C.C. and Keisler H. J. 1966. Continuous Model Theory, Princeton, Princeton University Press.
- Gerla G. 2001, Fuzzy logic: Mathematical Tools for Approximate Reasoning, Kluwer Academic Publishers, Dordrecht.
- Pavelka J. 1979, On fuzzy logic I: Many-valued rules of inference, Zeitschr. f. math. Logik und Grundlagen d. Math., 25, 45–52.
- Metcalfe, George; Olivetti, Nicola; Dov M. Gabbay (2008). Proof Theory for Fuzzy Logics. Springer. ISBN 978-1-4020-9408-8. Covers proof theory of many-valued logics as well, in the tradition of Hájek.
- Hähnle, Reiner (1993). Automated deduction in multiple-valued logics. Clarendon Press. ISBN 978-0-19-853989-6.
- Azevedo, Francisco (2003). Constraint solving over multi-valued logics: application to digital circuits. IOS Press. ISBN 978-1-58603-304-0.
- Bolc, Leonard; Borowik, Piotr (2003). Many-valued Logics 2: Automated reasoning and practical applications. Springer. ISBN 978-3-540-64507-8.
- Stanković, Radomir S.; Astola, Jaakko T.; Moraga, Claudio (2012). Representation of Multiple-Valued Logic Functions. Morgan & Claypool Publishers. doi:10.2200/S00420ED1V01Y201205DCS037. ISBN 978-1-60845-942-1.
External links
- Gottwald, Siegfried (2009). "Many-Valued Logic". Stanford Encyclopedia of Philosophy.
- Stanford Encyclopedia of Philosophy: "Truth Values"—by Yaroslav Shramko and Heinrich Wansing.
- IEEE Computer Society's Technical Committee on Multiple-Valued Logic
- Resources for Many-Valued Logic by Reiner Hähnle, Chalmers University
- Many-valued Logics W3 Server (archived)
- Yaroslav Shramko and Heinrich Wansing (2014). "Suszko's Thesis". Stanford Encyclopedia of Philosophy.
- Carlos Caleiro, Walter Carnielli, Marcelo E. Coniglio and João Marcos, Two's company: "The humbug of many logical values" in Jean-Yves Beziau, ed. (2007). Logica Universalis: Towards a General Theory of Logic (2nd ed.). Springer Science & Business Media. pp. 174–194. ISBN 978-3-7643-8354-1.
| ||||||||||||||||||||||||||||||
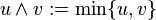
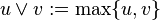
![\begin{align}
\neg_G u & =\begin{cases}
1, & \text{if }u=0\\
0, & \text{if }u>0
\end{cases}
\\
u \xrightarrow[G]{} v &= \begin{cases}
1, & \text{if }u\leq v\\
v, & \text{if }u>v
\end{cases}
\end{align}](../I/m/e33c6024c50915766d089de399f99919.png)

![u\xrightarrow[L]{} v:=min\{1,1-u+v\}](../I/m/7df4af188bcf920ed1176412cff5791b.png)
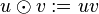
![u\xrightarrow[\Pi]{}v:=\begin{cases}
1, & \text{if }u\leq v\\
\frac {v}{u}, & \text{if }u>v
\end{cases}](../I/m/d60014e03cd59e5efc3c5b4b4f4f7354.png)
![\underset{\Pi}{\neg} u:= u \xrightarrow[\Pi]{}\overline{0}](../I/m/399d63945aacd784f0d20c152cc7ab4c.png)
![u \underset{\Pi}{\wedge} v:= u\odot (u \xrightarrow[\Pi]{} v)](../I/m/29f46144cf8c6a245183c84e8d30bf80.png)