Multi-compartment model
A multi-compartment model is a type of mathematical model used for describing the way materials or energies are transmitted among the compartments of a system. Each compartment is assumed to be a homogeneous entity within which the entities being modelled are equivalent. For instance, in a pharmacokinetic model, the compartments may represent different sections of a body within which the concentration of a drug is assumed to be uniformly equal.
Hence a multi-compartment model is a lumped parameters model.
Multi-compartment models are used in many fields including pharmacokinetics, epidemiology, biomedicine, systems theory, complexity theory, engineering, physics, information science and social science. The circuits systems can be viewed as a multi-compartment model as well.
In systems theory, it involves the description of a network whose components are compartments that represent a population of elements that are equivalent with respect to the manner in which they process input signals to the compartment.
- Instant homogeneous distribution of materials or energies within a "compartment."
- The exchange rate of materials or energies among the compartments is related to the densities of these compartments.
- Usually, it is desirable that the materials do not undergo chemical reactions while transmitting among the compartments.
- When concentration of the cell is of interest, typically the volume is assumed to be constant over time, though this may not be totally true in reality.
Most commonly, the mathematics of multi-compartment models is simplified to provide only a single parameter—such as concentration—within a compartment.
Single-compartment model
Possibly the simplest application of multi-compartment model is in the single-cell concentration monitoring (see the figure above). If the volume of a cell is V, the mass of solute is q, the input is u(t) and the secretion of the solution is proportional to the density of it within the cell, then the concentration of the solution C"' within the cell over time is given by
where k is the proportionality.
As the number of compartments increases, the model can be very complex and the solutions usually beyond ordinary calculation. Below shows a three-cell model with interlinks among each other.
The formulae for n-cell multi-compartment models become:
Where
 for
for  (as the total 'contents' of all compartments is constant in a closed system)
(as the total 'contents' of all compartments is constant in a closed system)
Or in matrix forms:
Where
 and
and  (as the total 'contents' of all compartments is constant in a closed system)
(as the total 'contents' of all compartments is constant in a closed system)
In the special case of a closed system (see below) i.e. where  then there is a general solution.
then there is a general solution.
Where  ,
,  , ... and
, ... and  are the eigenvalues of
are the eigenvalues of 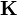 ;
;  ,
,  , ... and
, ... and  are the respective eigenvectors of
are the respective eigenvectors of 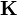 ; and
; and 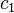 ,
, 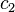 , .... and
, .... and  are constants.
are constants.
However it can be shown that given the above requirement to ensure the 'contents' of a closed system are constant, then for every pair of eigenvalue and eigenvector then either 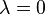 or
or  and also that one eigenvalue is 0, say
and also that one eigenvalue is 0, say 
So
Where
-
 for
for 
This solution can be rearranged:
This somewhat inelegant equation demonstrates that all solutions of an n-cell multi-compartment model with constant or no inputs are of the form:
Where 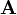 is a nxn matrix and
is a nxn matrix and  ,
, 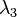 , ... and
, ... and  are constants.
Where
are constants.
Where 
Model topologies
Generally speaking, as the number of compartments increase, it is challenging both to find the algebraic and numerical solutions of the model. However, there are special cases of models, which rarely exist in nature, when the topologies exhibit certain regularities that the solutions become easier to find. The model can be classified according to the interconnection of cells and input/output characteristics:
- Closed model: No sinks or source, lit. all koi = 0 and ui = 0;
- Open model: There are sinks or/and sources among cells.
- Catenary model: All compartments are arranged in a chain, with each pool connecting only to its neighbors. This model has two or more cells.
- Cyclic model: It's a special case of the catenary model, with three or more cells, in which the first and last cell are connected, i.e. k1n ≠ 0 or/and kn1 ≠ 0.
- Mammillary model: Consists of a central compartment with peripheral compartments connecting to it. There are no interconnections among other compartments.
- Reducible model: It's a set of unconnected models. It bears great resemblance to the computer concept of forest as against trees.
See also
- Mathematical model
- Biomedical engineering
- Biological neuron models
- Compartmental models in epidemiology
- Physiologically-based pharmacokinetic modelling
References
- Godfrey, K., Compartmental Models and Their Application, Academic Press, 1983 (ISBN 0-12-286970-2).
- Anderson, D. H., Compartmental Modeling and Tracer Kinetics, Springer-Verlag Lecture Notes in Biomathematics #50, 1983 (ISBN 0-387-12303-2).
- Jacquez, J. A, Compartmental Analysis in Biology and Medicine, 2nd ed., The University of Michigan Press, 1985.
- Evans, W. C., Linear Systems, Compartmental Modeling, and Estimability Issues in IAQ Studies, in Tichenor, B., Characterizing Sources of Indoor Air Pollution and Related Sink Effects, ASTM STP 1287, pp. 239–262, 1996 (ISBN 0-8031-2030-3).






![\mathbf{q} =
\Bigg[ \mathbf{v_1}\begin{bmatrix}
c_1 & 0 & \cdots & 0 \\
\end{bmatrix}
+ \mathbf{v_2}\begin{bmatrix}
0 & c_2 & \cdots & 0 \\
\end{bmatrix}
+ \dots + \mathbf{v_n}\begin{bmatrix}
0 & 0 & \cdots & c_n \\
\end{bmatrix} \Bigg]
\begin{bmatrix}
1 \\
e^{\lambda_2t} \\
\vdots \\
e^{\lambda_nt} \\
\end{bmatrix}](../I/m/6954bc3b27a4b8b43f6380d2ed7320fc.png)
