Moving sofa problem

Unsolved problem in mathematics:
What is the largest area of a shape that can be maneuvered through a unit-width L-shaped corridor?
(more unsolved problems in mathematics)
The Hammersley sofa has area 2.2074... but is not the largest solution

The moving sofa problem was formulated by the Austrian-Canadian mathematician Leo Moser in 1966. The problem is a two-dimensional idealisation of real-life furniture moving problems, and asks for the rigid two-dimensional shape of largest area A that can be maneuvered through an L-shaped planar region with legs of unit width. The area A thus obtained is referred to as the sofa constant. The exact value of the sofa constant is an open problem.

Lower and upper bounds

As a semicircular disk of unit radius can pass through the corner, a lower bound for the sofa constant 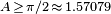\scriptstyle A\,\geq\,\pi/2\,\approx\, 1.57079 is readily obtained.

John Hammersley derived a considerably higher lower bound 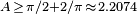\scriptstyle A\,\geq\,\pi/2 + 2/\pi\,\approx\,2.2074 based on a handset-type shape consisting of two quarter-circles of radius 1 on either side of a 1 by 4/π rectangle from which a semicircle of radius 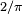\scriptstyle 2/\pi\, has been removed.[1][2]

Joseph Gerver found a sofa that further increased the lower bound for the sofa constant to approximately 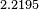\scriptstyle 2.2195.[3][4]

In a different direction, an easy argument by Hammersley shows that the sofa constant is at most 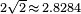\scriptstyle 2\sqrt{2}\,\approx\, 2.8284.[5][6]

See also

References

  1. ↑ Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1994). Hamos, Paul R., ed. Unsolved Problems in Geometry. Problem Books in Mathematics; Unsolved Problems in Intuitive Mathematics II. Springer-Verlag. ISBN 978-0-387-97506-1. Retrieved 24 April 2013.
  2. ↑ Moving Sofa Constant by Steven Finch at MathSoft, includes a diagram of Gerver's sofa
  3. ↑ Gerver, Joseph L. (1992). "On Moving a Sofa Around a Corner". Geometriae Dedicata 42 (3): 267–283. doi:10.1007/BF02414066. ISSN 0046-5755.
  4. ↑ Weisstein, Eric W., "Moving sofa problem", MathWorld.
  5. ↑ Wagner, Neal R. (1976). "The Sofa Problem" (PDF). The American Mathematical Monthly 83 (3): 188–189. doi:10.2307/2977022. JSTOR 2977022.
  6. ↑ Stewart, Ian (January 2004). Another Fine Math You've Got Me Into... Mineola, N.Y.: Dover Publications. ISBN 0486431819. Retrieved 24 April 2013.
This article is issued from Wikipedia - version of the Saturday, January 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.