Most-perfect magic square

੭	੧੨	੧	੧੪
੨	੧੩	੮	੧੧
੧੬	੩	੧०	੫
੯	੬	੧੫	੪

7	12	1	14
2	13	8	11
16	3	10	5
9	6	15	4

transcription of
the indian numerals

Most-perfect magic square from
the Parshvanath Jain temple in Khajuraho

A most-perfect magic square of order n is a magic square containing the numbers 1 to n² with two additional properties:

Each 2×2 subsquare sums to 2s, where s = n² + 1.
All pairs of integers distant n/2 along a (major) diagonal sum to s.

Examples

Specific examples of most-perfect magic squares that begin with the 2015 date demonstrate how theory and computer science are able to define this group of magic squares. ^[1]^[2] Only a fraction of the 2x2 cell blocks that sum to 130 are accented by the different colored fonts in the 8x8 example.

The 12x12 square below was found by making all the 42 principal reversible squares with ReversibleSquares, running Transform1 2All on all 42, making 23040 of each, (of the 23040 x 23040 total each), then making the most-perfect squares from these with ReversibleMost-Perfect. These squares were then scanned for squares with 20,15 in the proper cells for any of the 8 rotations. The 2015 squares all originated with principal reversible square number #31. This square has values that sum to 35 on opposite sides of the vertical midline in the first two rows.^[2]

12 × 12 Most-Perfect Magic Square
20	15	60	49	24	51	132	123	92	89	128	87
119	136	79	102	115	100	7	28	47	62	11	64
25	10	65	44	29	46	137	118	97	84	133	82
126	129	86	95	122	93	14	21	54	55	18	57
31	4	71	38	35	40	143	112	103	78	139	76
113	142	73	108	109	106	1	34	41	68	5	70
13	22	53	56	17	58	125	130	85	96	121	94
138	117	98	83	134	81	26	9	66	43	30	45
8	27	48	61	12	63	120	135	80	101	116	99
131	124	91	90	127	88	19	16	59	50	23	52
2	33	42	67	6	69	114	141	74	107	110	105
144	111	104	77	140	75	32	3	72	37	36	39

12 x 12 reversible square #31 of 42
1	2	7	8	13	14	19	20	25	26	31	32
3	4	9	10	15	16	21	22	27	28	33	34
5	6	11	12	17	18	23	24	29	30	35	36
37	38	43	44	49	50	55	56	61	62	67	68
39	40	45	46	51	52	57	58	63	64	69	70
41	42	47	48	53	54	59	60	65	66	71	72
73	74	79	80	85	86	91	92	97	98	103	104
75	76	81	82	87	88	93	94	99	100	105	106
77	78	83	84	89	90	95	96	101	102	107	108
109	110	115	116	121	122	127	128	133	134	139	140
111	112	117	118	123	124	129	130	135	136	141	142
113	114	119	120	125	126	131	132	137	138	143	144

Physical Properties

The image below shows numbers completely surrounded by larger numbers with a blue background.

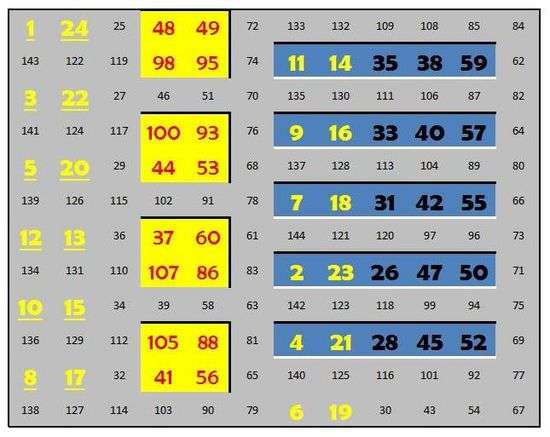Magic Space

The Hilbert space filling curve can be divided into 8 cell segments. Each of these segments can be labeled from the beginning of the segment to the end of the segment with the numbers 1 - 8 (b). There are 144 examples of the 8x8 most-perfect magic squares where the 8 cell segments sum to the magic constant of 260 as well as the individual positions in each segment summing to 260. The 1st position is highlighted with a large red font in b) and c) below. The Hilbert curve in a sequential one dimensional representation can be folded and bent into a 2 or 3 dimensional structure. Thus this curve can serve as a Rosetta stone to transition between 2D and 3D magic spaces.^[3]

Properties

All most-perfect magic squares are panmagic squares.

Apart from the trivial case of the first order square, most-perfect magic squares are all of order 4n. In their book, Kathleen Ollerenshaw and David S. Brée give a method of construction and enumeration of all most-perfect magic squares. They also show that there is a one-to-one correspondence between reversible squares and most-perfect magic squares.

For n = 36, there are about 2.7 × 10⁴⁴ essentially different most-perfect magic squares.

The second property above implies that each pair of the integers with the same background colour in the 4×4 square below have the same sum, and hence any 2 such pairs sum to the magic constant.

7	12	1	14
2	13	8	11
16	3	10	5
9	6	15	4

Notes

References

Kathleen Ollerenshaw, David S. Brée: Most-perfect Pandiagonal Magic Squares: Their Construction and Enumeration, Southend-on-Sea : Institute of Mathematics and its Applications, 1998, 186 pages, ISBN 0-905091-06-X
T.V.Padmakumar, Number Theory and Magic Squares, Sura books, India, 2008, 128 pages, ISBN 978-81-8449-321-4

External links

T. V. Padmakumar, Strongly magic squares
Harvey Heinz: Most-perfect Magic Squares
A051235, number of essentially different most-perfect pandiagonal magic squares of order 4n, at the On-Line Encyclopedia of Integer Sequences

This article is issued from Wikipedia - version of the Monday, January 11, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.