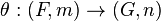Monoidal natural transformation

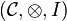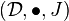Suppose that $(\mathcal C,\otimes,I)$ and $(\mathcal D,\bullet, J)$ are two monoidal categories and

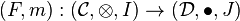(F,m):(\mathcal C,\otimes,I)\to(\mathcal D,\bullet, J)

and

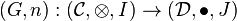
(G,n):(\mathcal C,\otimes,I)\to(\mathcal D,\bullet, J)

are two lax monoidal functors between those categories.

A monoidal natural transformation

\theta:(F,m) \to (G,n)

between those functors is a natural transformation 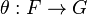$\theta:F \to G$ between the underlying functors such that the diagrams

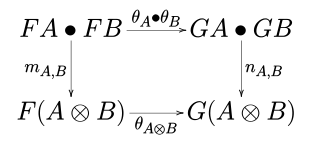and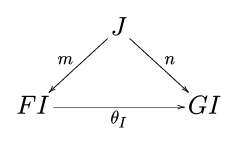

commute for every objects $A$ and $B$ of $\mathcal C$ (see Definition 11 in ^[1]).

A symmetric monoidal natural transformation is a monoidal natural transformation between symmetric monoidal functors.

References

↑ Baez, John C. "Some Definitions Everyone Should Know" (PDF). Retrieved 2 December 2014.

This article is issued from Wikipedia - version of the Wednesday, December 03, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.