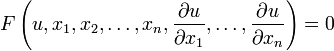Monge equation
In the mathematical theory of partial differential equations, a Monge equation, named after Gaspard Monge, is a first-order partial differential equation for an unknown function u in the independent variables x1,...,xn
that is a polynomial in the partial derivatives of u. Any Monge equation has a Monge cone.
Classically, putting u = x0, a Monge equation of degree k is written in the form
and expresses a relation between the differentials dxk. The Monge cone at a given point (x0, ..., xn) is the zero locus of the equation in the tangent space at the point.
The Monge equation is unrelated to the (second-order) Monge–Ampère equation.
This article is issued from Wikipedia - version of the Friday, February 08, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.